Name: 
 

Math 10 Foundations LG 15 Practice Quiz 2


Multiple Choice
Identify the choice that best completes the statement or answers the question.
 

 1. 
Determine tan A and tan C.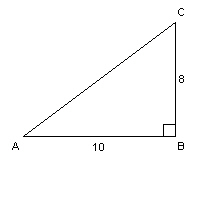
mc001-1.jpg
a.
tan A = 1.25; tan C = 0.8
c.
tan A = 0.8; tan C = 1.25
b.
tan A = 0.8; tan C = 0.7809...
d.
tan A = 0.6247...; tan C = 1.25
 

 2. 
Determine the measure of ÐABD to the nearest tenth of a degree.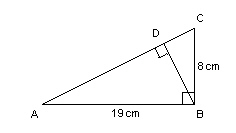
mc002-1.jpg
a.
65.1°
b.
67.2°
c.
22.8°
d.
24.9°
 

 3. 
Determine the length of side z to the nearest tenth of a centimetre.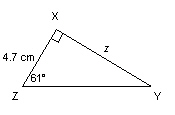
mc003-1.jpg
a.
9.7 cm
b.
2.6 cm
c.
5.4 cm
d.
8.5 cm
 

 4. 
A ladder leans against a wall. The base of the ladder is on level ground 1.2 m from the wall. The angle between the ladder and the ground is 70°. How far up the wall does the ladder reach, to the nearest tenth of a metre?
a.
0.4 m
b.
1.3 m
c.
3.5 m
d.
3.3 m
 

 5. 
Terry is lying on the ground near the B.C. Legislature Building. The angle between the ground and his line of sight to the highest point on the building is 53°. The height of the building, from the ground to its highest point, is about 43 m. About how far is Terry from a point on the ground vertically below the highest point on the building? Give the answer to the nearest metre.
a.
71 m
b.
57 m
c.
34 m
d.
32 m
 

 6. 
A flagpole casts a shadow that is 21 m long when the angle between the sun’s rays and the ground is 48°. Determine the height of the flagpole, to the nearest metre.
a.
19 m
b.
16 m
c.
14 m
d.
23 m
 

 7. 
The angle between one shorter side of a rectangle and a diagonal is 64°. One longer side of the rectangle is 9.2 cm. What is the width of the rectangle, to the nearest tenth of a centimetre?
a.
4.0 cm
b.
18.9 cm
c.
8.3 cm
d.
4.5 cm
 

 8. 
From a point 18 ft. from the base of a flagpole, Seema used a clinometer to sight the top of the flagpole. Seema held the clinometer 5 ft. 3 in. above the ground. The angle between the horizontal and the line of sight was 52°. Determine the height of the flagpole to the nearest foot.
a.
28 ft.
b.
34 ft.
c.
19 ft.
d.
23 ft.
 

 9. 
Determine sin A and cos A to the nearest tenth.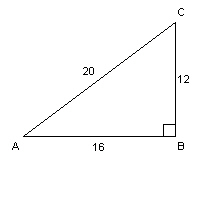
mc009-1.jpg
a.
sin A = 1.7;  cos A = 0.8
c.
sin A = 0.6;  cos A = 1.3
b.
sin A = 0.8;  cos A = 0.6
d.
sin A = 0.6;  cos A = 0.8
 

 10. 
Determine the measure of ÐQ to the nearest tenth of a degree.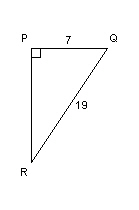
mc010-1.jpg
a.
68.4°
b.
69.8°
c.
21.6°
d.
20.2°
 

 11. 
A rectangle is 5.1 cm wide and each diagonal is 9.3 cm long. What is the measure of the angle between a diagonal and the shorter side of the rectangle to the nearest tenth of a degree?
a.
33.3°
b.
61.3°
c.
56.7°
d.
28.7°
 

 12. 
The route along the Kettle Valley Railway rises approximately 850.0 m from Penticton to Chute Lake. The distance measured along this route is 43.6 km. Assume this is a straight path. Determine the angle of inclination of the path to the nearest tenth of a degree.
a.
88.9°
b.
2.9°
c.
11.2°
d.
1.1°
 

 13. 
A ladder is 8.0 m long. It leans against a wall. The angle of inclination of the ladder is 72°. To the nearest tenth of a metre, how far from the wall is the base of the ladder?
a.
2.6 m
b.
7.6 m
c.
25.9 m
d.
2.5 m
 

 14. 
Solve this right triangle. Give the measures to the nearest tenth.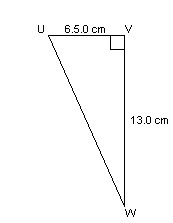
mc014-1.jpg
a.
mc014-2.jpg cm
c.
mc014-4.jpg cm
b.
mc014-3.jpg cm
d.
mc014-5.jpg cm
 

 15. 
Solve this right triangle. Give the measures to the nearest tenth.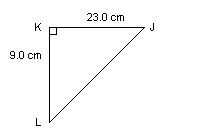
mc015-1.jpg
a.
mc015-2.jpg cm
c.
mc015-4.jpg cm
b.
mc015-3.jpg cm
d.
mc015-5.jpg cm
 

 16. 
Determine the length of this wheelchair ramp to the nearest hundredth of a metre.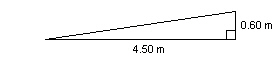
mc016-1.jpg
a.
4.60 m
b.
7.50 m
c.
4.46 m
d.
4.54 m
 

 17. 
A road rises 1 m for every 19 m measured along the road. To the nearest metre, how far does a car travel horizontally when it travels 300 m along the road?
a.
300 m
b.
16 m
c.
19 m
d.
300 m
 

 18. 
Determine the area of this rectangle to the nearest tenth of a square metre.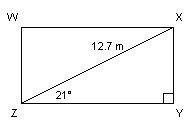
mc018-1.jpg
a.
54.0 m2
b.
420.2 m2
c.
98.1 m2
d.
61.9 m2
 

 19. 
Two trees are 55 yd. apart. From a point halfway between the trees, the angles of elevation of the tops of the trees are measured. What is the height of each tree to the nearest yard?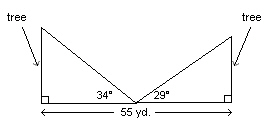
mc019-1.jpg
a.
33 yd.; 31 yd.
c.
41 yd.; 50 yd.
b.
19 yd.; 15 yd.
d.
40 yd.; 49 yd.
 

 20. 
From the top of an 80-ft. building, the angle of elevation of the top of a taller building is 49° and the angle of depression of the base of this building is 62°. Determine the height of the taller building to the nearest foot.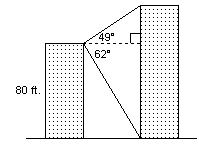
mc020-1.jpg
a.
211 ft.
b.
112 ft.
c.
129 ft.
d.
276 ft.
 

Short Answer
 

 21. 
A road increases 8 m in altitude for every 100 m of horizontal distance. Calculate the angle of inclination of the road, to the nearest tenth of a degree.
 

 22. 
a) For ÐM in the triangle below, label the hypotenuse and the opposite and adjacent sides.
b) Determine tan M to the nearest hundredth.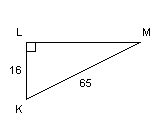
sa022-1.jpg
 

 23. 
A communications tower is 300 m high. Rebecca is driving toward the tower. The angle between the ground and Rebecca’s line of sight to the top of the tower is 5°. About how far is Rebecca from a point on the ground vertically below the top of the tower, to the nearest hundred metres?
 

 24. 
A flagpole is 14.0 m high. At a certain point, the angle between the ground and Jon’s line of sight to the top of the flagpole is 63°. About how far is Jon from the flagpole, to the nearest tenth of a metre?
 

 25. 
A ladder is 7 m long. It leans against a house. The base of the ladder is 2 m from the house. What is the angle of inclination of the ladder to the nearest tenth of a degree?
 

Problem
 

 26. 
Determine the measures of 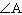pr026-1.jpg and 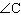pr026-2.jpg to the nearest tenth of a degree.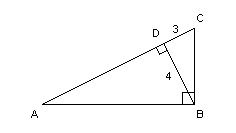
pr026-3.jpg
 

 27. 
Guy wires are attached to buildings as shown. A student says the angles of inclination of the wires are the same. Is the student correct? Justify your answer.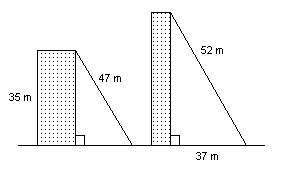
pr027-1.jpg
 

 28. 
Determine the area of this right triangle to the nearest square metre.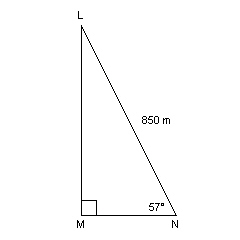
pr028-1.jpg
 

 29. 
Determine the perimeter of this triangle to the nearest tenth of a centimetre.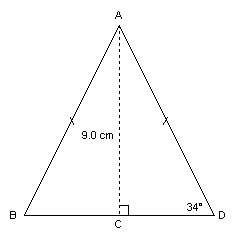
pr029-1.jpg
 

 30. 
Determine the length of the diagonals in this kite to the nearest tenth of a centimetre.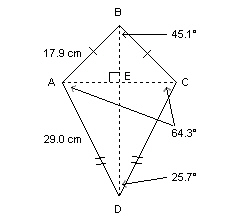
pr030-1.jpg
 



 
Check Your Work     Start Over