Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
One side of a square is 19h in length. What is the area of the
square?
|
|
|
2.
|
Which statement is correct about the expression 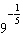 when it is
evaluated? a. | The expression is equal to 0. | b. | The sign is positive | c. | The sign is
negative | d. | The expression is undefined. |
|
|
|
3.
|
For what value of x do 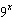 , 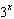 , and 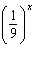 have the same
value? a. | x = 0 | b. | 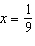 | c. | x =
9 | d. | x = 3 |
|
|
|
4.
|
Determine the value of y in the equation y = 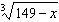 when x
= 122. Leave your answer in simplest radical form if necessary.
|
|
|
5.
|
Which expression has the largest value?
|
|
|
6.
|
Order these irrational numbers from least to greatest: 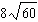 , 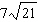 ,
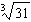 , 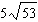 . a. | 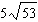 , , 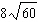 , , 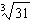 ,, ,, 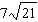 | b. | 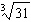 , , 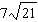 , , 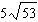 , , 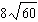 | c. | 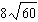 , , 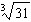 , , 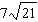 , , 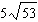 | d. | 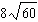 , , 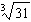 , , 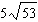 , , 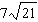 |
|
|
|
7.
|
Determine the product (x + 7)(x + 9).
a. | x2 + 7x + 63 | b. | x2 + 63x +
16 | c. | x2 + 16x + 63 | d. | x2 + 63x +
63 |
|
|
|
8.
|
The area of a rectangle is given as x2 – 7x
– 30. What is the length of one side of the rectangle?
a. | x – 30 | b. | x + 30 | c. | x +
3 | d. | x – 3 |
|
|
|
9.
|
What value of k makes the trinomial 36x2 + kx +
81 a perfect square?
|
|
|
10.
|
The area, in metres, of a rectangle is 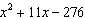 . When the expression
is factored fully, the factors are the dimensions of the rectangle. Determine the actual dimensions,
in metres, of the rectangle when x = 36. a. | 17 m by 58 m | b. | 41 m by 17 m | c. | 18 m by 41
m | d. | 24 m by 59 m |
|
|
|
11.
|
What is the factored form of 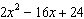 ?
|
|
|
12.
|
Which multiplication statement is represented by the algebra tiles
below? 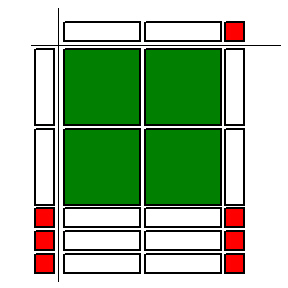
|
|
|
13.
|
Which statement describes what is happening to the skier as she moves from point
C to D on the graph? 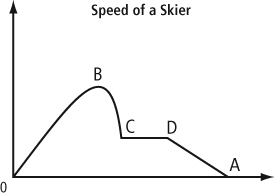 a. | The skier is increasing speed at a constant rate. | b. | The skier is slowing
down and has stopped. | c. | The skier is travelling at a constant
speed. | d. | The skier has reached her maximum speed. |
|
|
|
14.
|
Given the equation 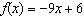 , determine 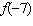 .
|
|
|
15.
|
Evaluate 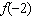 for the function 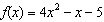 .
|
|
|
16.
|
The rate of change of a vertical line is
a. | negative | b. | zero | c. | undefined | d. | positive |
|
|
|
17.
|
Which statement is not true about lines 1 and 2? 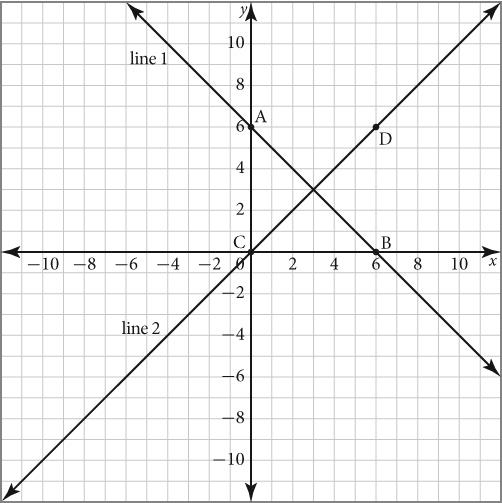 a. | Line 2 is steeper than Line 1. | b. | Line 1 has a negative
slope. | c. | Line 2 has a positive slope. | d. | Line 1 and Line 2 are
perpendicular. |
|
|
|
18.
|
Which of the following line segment(s) have a zero slope? 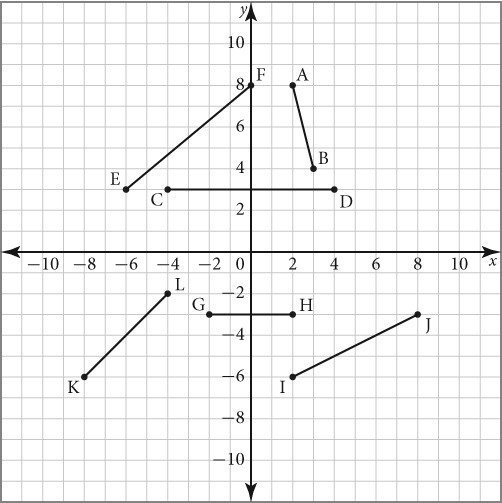 a. | Line segments IJ, GH, and KL | b. | Line segments CD and GH | c. | Line segments EF,
KL, and IJ | d. | Line segment AB |
|
|
|
19.
|
Which of the following is equivalent to the equation 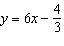 ?
|
|
|
20.
|
Rewrite the equation 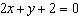 in slope-intercept form.
|
|
|
21.
|
Identify the slope and y-intercept of the relation represented by the
equation 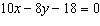 .
|
|
|
22.
|
Points A 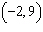 and B 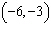 are on a line. What is the equation of the
line?
|
|
|
23.
|
What is the value of p in the equation of the line 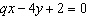 , such that
the x-intercept is –16?
|
|
|
24.
|
Using the table of values, determine the y-intercept of the
line.
|
|
|
25.
|
Which of the following linear systems has the solution 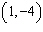 .
|
|
|
26.
|
What is the y-coordinate for the intersection point in the linear system
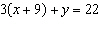 and 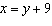 ?
|
|
|
27.
|
Use the elimination method. The solution to the linear system 16x +
7y = –145 and –8x + 7y = –1 is
a. | (–6, –7) | b. | (6, –7) | c. | (–6,
7) | d. | (6, 7) |
|
|
|
28.
|
Emily babysits for a fee of $34.50 for one evening plus $1.15 per diaper change.
Cindy charges $27.60 for one evening plus $2.30 per diaper change. How many diapers does each girl
have to change in order to charge the same total fee?
|
|
|
29.
|
Matthew has a jar of coins in which he places quarters and dimes. There are
twice as many quarters as dimes in the jar. The total amount in the jar is $42.00. How many of each
coin does Matthew have?
a. | 168 quarters and 0 dimes | b. | 0 quarters and 420 dimes | c. | 70 quarters and 140
dimes | d. | 140 quarters and 70 dimes |
|
|
|
30.
|
In the triangle , WG = 16 cm and tan G = 0.375. What is the length
of the hypotenuse, to the nearest tenth of a centimetre? 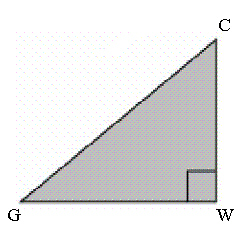 a. | 17.1 cm | b. | 6.0 cm | c. | 22.0
cm | d. | 42.7 cm |
|
|
|
31.
|
Evaluate tan 90°.
|
|
|
32.
|
Determine the measure of 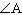 , to the nearest degree. 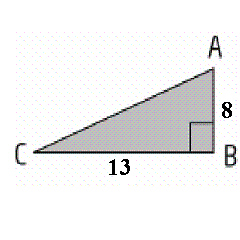
|
|
|
33.
|
A surveyor, S, is measuring the width of a street, using a marker, M. The
surveyor cannot measure the width directly, because there is too much traffic. She stands on the east
side of the intersection. The marker is on the west side of the intersection, and is 18 m north of
the intersection. Determine the width of the street, to the nearest tenth of a
metre. 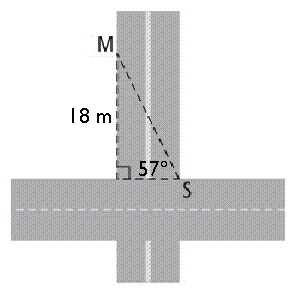 a. | 33.0 m | b. | 21.5 m | c. | 11.7
m | d. | 27.7 m |
|
|
|
34.
|
In 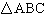 , AC = 7 cm and BC = 13 cm. Determine the sine ratio of  A, to the nearest thousandth. 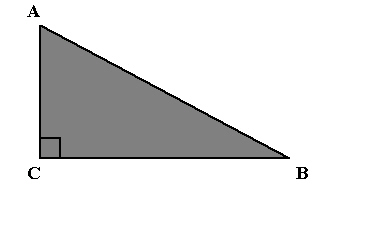 a. | 0.880 | b. | 0.474 | c. | 0.538 | d. | 1.857 |
|
|
|
35.
|
If 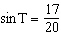 , what is the measure of 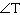 , to the nearest
degree?
|
|
|
36.
|
The Canada Pension Plan (CPP) employee contribution rate is 4.95% of a
person’s gross pay up to a maximum of $2593.80 per year. The employer’s contribution rate
is 4.95% of a person’s gross pay up to a maximum of $2593.80 per year. How much did the
government collect in CPP payments for the year if the employee made $74 000.00 for the year?
a. | $2593.80 | b. | $3890.70 | c. | $5187.60 | d. | $3663.00 |
|
|
|
37.
|
The Employment Insurance (EI) rate is 1.66% of a person’s gross pay up to
a maximum of $858.22 per year. The employer’s contribution rate is 2.32% of a person’s
gross pay up to a maximum of $1201.51 per year. How much did the employer pay in premiums if
Catherine makes $34 000.00 for the year?
a. | $564.40 | b. | $858.22 | c. | $1353.20 | d. | $788.80 |
|
|
|
38.
|
Erek works at a stationary store on Saturday night where he earns $280.15 per
month. Erek uses this money to pay for his cell phone plan that is $68/month, a transit pass for
$58/month, and a karate class for $56/month. How much money will he have left after expenses?
a. | $214.15 | b. | $98.15 | c. | $86.15 | d. | $210.15 |
|
|
|
39.
|
Erek works at a local restaurant earning $12.10/h. He is paid time-and-a-half
for any hours above a 40-h work week. Erek works the following hours earns the following in tips.
| Day | Hours Worked | Tips | | Monday | 0 | $0 | | Tuesday | 6 | $25 | | Wednesday | 0 | $0 | | Thursday | 10.5 | $84 | | Friday | 0 | $0 | | Saturday | 0 | $0 | | Sunday | 0 | $0 | | | |
What is his gross pay for
the week if he is required to give 2% of his tips to the kitchen staff? a. | $408.48 | b. | $306.47 | c. | $308.65 | d. | $199.65 |
|
|
|
40.
|
Jin receives a pay stub from his job as a writer/editor. He is paid bi-weekly.
Earnings Statement Employee Name: Garcia, Jin Occupation: Athletic Trainer Period
End Date: June 18 Cheque Number: 1394 | Earnings | | | | | Deductions | | | Description | Hours | Rate | Amount | | Description | Amount | | Regular
Hours | 80 | 18.50 | 1480.00 | | Income Tax | 1664.76 | | Overtime | 20 | 27.75 | 555.00 | | EI | 33.01 | | Overtime | 44 | 37.00 | 1628.00 | | CPP | 99.76 | | Vacation
Pay | | | 146.52 | | | | | Gross Pay | | | 3809.52 | | Total Deductions | 1797.53 | | | | | | | Net
Pay | 2011.99 | | | | | | | |
What
is Jin’s gross pay for the year? a. | $198 095.04 | b. | $45 714.24 | c. | $99
047.52 | d. | $91 428.48 |
|
Short Answer
|
|
|
1.
|
Brian is a lab technician. His regular pay is $25.70/h. If he works on a
holiday, he receives a shift premium of double-time for those hours. Determine how many hours he
worked on the holiday if his gross pay for the following week is $1207.90. | Sunday | Monday - Holiday | Tuesday | Wednesday | Thursday | Friday | Saturday | | 10 h | ____ h | Day Off | Day Off | 8 h | 9 h | 8
h | | | | | | | |
|
|
|
2.
|
Frazer is hired as a lifeguard and earns $24.25/h with a 3.75 h work day. The
position is unionized with 1.25% deducted for union dues. How much money would Frazer pay in union
dues each working day?
|
|
|
3.
|
Owen decides to go parasailing while on vacation. The flyer advertises that the
maximum height reached during the trip will be 51 m. If the parasailing cable is 92 m long, what
angle will the cable make with the horizontal when Owen reaches the maximum height? Express your
answer to the nearest degree.
|
|
|
4.
|
Factor the trinomial 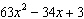 .
|
|
|
5.
|
Company A charges an initial setup fee of $105 and $25 a month for internet.
Company B charges an initial setup fee of $75 and $30 a month for internet. After how many months
would the two options cost the same?
|
Problem
|
|
|
1.
|
Claude is a sales consultant for a mail-order jewelry company and earns 20% of
his sales. If he sells more than $3800 in a week, he earns a $400 bonus. Last week, Claude sold the
following amounts each day. (Hint: Round Claude’s gross salary to the nearest dollar.) | Monday | $1007.00 | | Tuesday | $652.00 | | Wednesday | $944.00 | | Thursday | $760.00 | | Friday | $1181.00 | | |
Assuming Claude has the same gross pay each week and takes 8 weeks
of vacation, what is Claude’s net pay for the year? 2018 British Columbia: Provincial
Income Tax Amounts | Income | Tax Rate | | $0 – $38 898 | 5.06% | | $38 898 – $77 797 | 7.7% | | $77 797 – $89 320 | 10.5% | | $89 320 – $108 460 | 12.29% | | over $108 460 | 14.7% | | |
2018 Canada: Federal
Income Tax Amounts | Income | Tax Rate | | $0 – $45 916 | 15% | | $45 916 - $91 831 | 20.5% | | $91 831 - $142 353 | 26% | | $142 353 - $202 800 | 29% | | over $202 800 | 33% | | |
Employment Insurance
(EI) Premium Rate: 1.66% to a maximum of $858.22 Canada Pension Plan (CPP) Contribution Rate:
4.95% to a maximum of $2593.80
|
|
|
2.
|
Harper works at Purse World. For one day of work she earns 10% commission on
every purse she sells, plus her daily wage of $50. Each purse sells for $60. a) Make a
table of values to represent Harper’s earnings for 0 to 5 purses sold. b) Graph
the relation.  c) c) Is the relation a function?
Explain. d) What is the slope of the graph? What does it
represent e) The equation 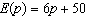 can be used to represent this
situation. How many purses does Sara have to sell to earn $194 in a day?
|
|
|
3.
|
A long-distance phone service charges $14 a month plus $0.15/min of call
time.
a) Write an equation in general form that represents the total monthly charge,
C, in dollars, in terms of call time, t, in minutes.
b) If the monthly charge
were increased to $17, what would the new equation be?
c) What is the relationship between
the graphs of the equations from parts a) and b)?
|
|
|
4.
|
Charlotte is travelling out of the country for spring break and wants to
investigate whether getting an international text messaging plan is worth it. Her currently provider
will charge her $0.20 for each text message she sends and $0.10 for each text message she receives.
She can pay $35 for unlimited international texting while she is away. What number of text messages
can she send and receive so that purchasing the unlimited package is more cost effective? Use a graph
to support your answer. 
|