Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
What is 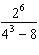 ?
|
|
|
2.
|
Simplify 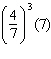 . a. | 448 | b. | 64 | c. | 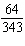 | d. | 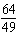 |
|
|
|
3.
|
Which expression represents a negative number?
|
|
|
4.
|
Which point is not located above the x-axis on a coordinate grid?
|
|
|
5.
|
Determine the value of y in the equation y = 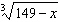 when x
= 122. Leave your answer in simplest radical form if necessary.
|
|
|
6.
|
Express 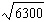 as an equivalent mixed radical.
|
|
|
7.
|
Rhada’s bedroom floor has a width equal to 10x + 5 and a length
equal to 5x – 7. What equation represents the area of the floor?
a. | A = 50x2 + 95x – 35 | b. | A =
50x2 + 45x – 35 | c. | A = 50x2 –
95x – 35 | d. | A = 50x2 –
45x – 35 |
|
|
|
8.
|
The expression –65x2 – 10x + 10 written in
factored form is
a. | –5(13x2 + 2x – 2) | b. | –5(–13x2 – 2x + 2) | c. | –5(–13x2 + 2x – 2) | d. | –5(13x2 – 2x +
2) |
|
|
|
9.
|
What is the expression –110x2 + 40x – 30 in
factored form?
a. | –10(11x2 + 4x – 3) | b. | –10(11x2 – 4x + 3) | c. | –10(–11x2 + 4x – 3) | d. | –10(–11x2 – 4x +
3) |
|
|
|
10.
|
What is the factored form of the expression 4x2 + 44?
a. | 4(x2 + 11) | b. | 4x2(x +
11) | c. | 4x(x2 + 11) | d. | 4x(x +
11) |
|
|
|
11.
|
Factor x2 – 169.
a. | (x + 13)(x – 13) | b. | (x + 13)(x +
13) | c. | cannot be factored | d. | (x – 13)(x –
13) |
|
|
|
12.
|
Suppose the area of a rectangle is represented by the expression
100x2 – 49. When the expression is fully factored, the factors represent the
dimensions of the rectangle. What expressions represent the dimensions of the rectangle?
a. | 10x + 7 and 10x – 7 | b. | 10x + 7 and
10x + 7 | c. | 10 and 10x2 – 49 | d. | 10x – 7
and 10x – 7 |
|
|
|
13.
|
Benjamin starts walking to a friend’s house and gradually increases his
speed until he gets there. After visiting for a short time, Benjamin and his friend start walking
back to Benjamin’s house. On the way, they meet up with a third friend. The three boys continue
to walk at a slower pace. When Benjamin realizes that he is late, he starts walking at a faster
constant rate until he gets home. Which distance-time graph represents this situation?
|
|
|
14.
|
The cost of a taxi ride is $6.00 plus $0.25 for every 0.5 km. Which graph
represents this relation?
|
|
|
15.
|
Evaluate 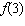 for the function 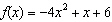 .
|
|
|
16.
|
Which statement is not true?
a. | All functions are relations. | b. | Each function has its own rule that is often
given using function notation. | c. | A relation is a function if each value in the
domain corresponds to exactly one value in the range. | d. | All relations are
functions. |
|
|
|
17.
|
Determine the slope of the line that passes through the points 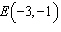 and 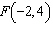
are on a line. What is the run from point E to point F?
|
|
|
18.
|
Use the table of values to determine the slope of the relation.
x | y | –6 | –1 | –8 | 2 | –10 | 5 | –12 | 8 | –14 | 11 | –16 | 14 | | |
|
|
|
19.
|
The slope of the line 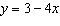 is
|
|
|
20.
|
Elizabeth invested $500 in an account that pays 5% simple interest per year. The
equation representing Elizabeth’s investment is A = P + Prt, where
A is the value of the investment, in dollars, P is the starting principle amount, in
dollars, r is the interest rate written as a decimal, and t is the number of years the
money is invested. What is the value of the investment after 40 years?
a. | $1000 | b. | $10500 | c. | $1500 | d. | $100500 |
|
|
|
21.
|
Points C 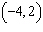 and D 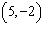 are on a line. What is the run from point
C to D?
|
|
|
22.
|
Points A 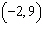 and B 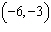 are on a line. What is the equation of
the line?
|
|
|
23.
|
What is the value of p in the equation of the line 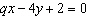 , such
that the x-intercept is –16?
|
|
|
24.
|
Identify the pair of perpendicular lines.
|
|
|
25.
|
Determine the x-coordinate that is a solution to the linear system
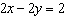 and 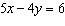 .
|
|
|
26.
|
Which of the following linear systems has the solution 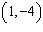 .
|
|
|
27.
|
Determine the solution to the linear system 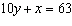 and 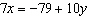 , using the
substitution method.
|
|
|
28.
|
The perimeter of a rectangle is 58 m. The length is 4 m less than twice the
width. What is the length of the rectangle?
|
|
|
29.
|
During the summer, Evelyn mows lawns for her neighbours. He charges $8 per lawn.
Landscape Designs charges $97 for the entire season. How many times would Evelyn need to cut a lawn
before her fee is more than that charged by Landscape Designs?
|
|
|
30.
|
A right triangle has legs measuring 12 cm and 5 cm. The length of the hypotenuse
is
a. | 17 cm | b. | 13 cm | c. | 8
cm | d. | 169 cm |
|
|
|
31.
|
In the triangle , WG = 16 cm and tan G = 0.375. What is the length
of the hypotenuse, to the nearest tenth of a centimetre? 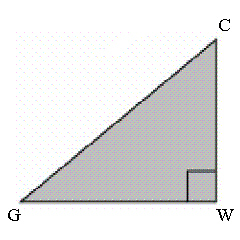 a. | 17.1 cm | b. | 6.0 cm | c. | 22.0
cm | d. | 42.7 cm |
|
|
|
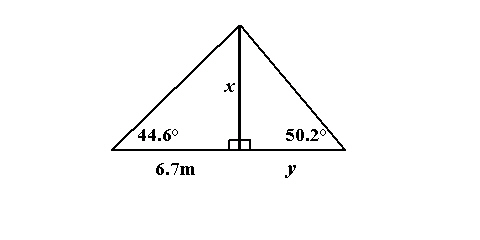
Use the diagram to answer the following question(s).
|
|
|
32.
|
Determine the length of x, to the nearest tenth of a metre.
a. | 6.6 m | b. | 11.2 m | c. | 12.8
m | d. | 5.5 m |
|
|
|
33.
|
If sin A = 0.5592, then the measure of  A, to the nearest degree,
is
|
|
|
34.
|
What is the cosine ratio of 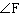 ? ?
|
|
|
35.
|
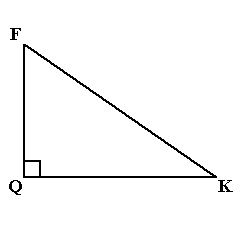
Determine the length of x and the length of y, to the nearest
tenth of a metre.  a. | x = 8.9 m and y = 10.2 m | b. | x = 8.9 m and y = 13.4
m | c. | x = 10.2 m and y = 5.0 m | d. | x = 13.4 m and y = 10.0
m |
|
|
|
36.
|
Catherine works as a realtor and earns 2.75% commission on a home sale. If she
earns $19 420.34 on the sale, what was the selling price of the house?
a. | $70 619.40 | b. | $534 059.21 | c. | $53
405.92 | d. | $706 194.00 |
|
|
|
37.
|
On a recent 4.75-h shift a DJ earns $11.45/h plus $39.75 in tips. If 30% is
deducted and transferred to a savings account to be saved towards a school trip how much money will
she save from the shift?
a. | $24.81 | b. | $28.24 | c. | $16.79 | d. | $25.67 |
|
|
|
38.
|
Cai earns an annual salary of $73 000. Her total deductions for the year are $14
965.00, $5621.00, $2593.80, and $858.22 for federal tax, provincial tax, CPP, and EI, respectively
each year. What were Cai’s total deductions for the year?
a. | $24 038.02 | b. | $78 891.98 | c. | $48
961.98 | d. | $73 000.00 |
|
|
|
39.
|
Erek works at a local restaurant earning $12.10/h. He is paid time-and-a-half
for any hours above a 40-h work week. Erek works the following hours earns the following in tips.
| Day | Hours Worked | Tips | | Monday | 0 | $0 | | Tuesday | 6 | $25 | | Wednesday | 0 | $0 | | Thursday | 10.5 | $84 | | Friday | 0 | $0 | | Saturday | 0 | $0 | | Sunday | 0 | $0 | | | |
What is his gross pay for
the week if he is required to give 2% of his tips to the kitchen staff? a. | $408.48 | b. | $306.47 | c. | $308.65 | d. | $199.65 |
|
|
|
40.
|
Jin receives a pay stub from his job as a writer/editor. He is paid bi-weekly.
Earnings Statement Employee Name: Garcia, Jin Occupation: Athletic Trainer Period
End Date: June 18 Cheque Number: 1394 | Earnings | | | | | Deductions | | | Description | Hours | Rate | Amount | | Description | Amount | | Regular
Hours | 80 | 18.50 | 1480.00 | | Income Tax | 1664.76 | | Overtime | 20 | 27.75 | 555.00 | | EI | 33.01 | | Overtime | 44 | 37.00 | 1628.00 | | CPP | 99.76 | | Vacation
Pay | | | 146.52 | | | | | Gross Pay | | | 3809.52 | | Total Deductions | 1797.53 | | | | | | | Net
Pay | 2011.99 | | | | | | | |
What
is Jin’s gross pay for the year? a. | $198 095.04 | b. | $45 714.24 | c. | $99
047.52 | d. | $91 428.48 |
|
Short Answer
|
|
|
1.
|
Quon is hired as a data entry clerk and earns $25.00/h with a 7.75 h work day.
The position is unionized with 1.00% deducted for union dues. In addition, income tax of
$29.06, CPP contributions of $9.59, and EI of $3.22. What is Quon’s net pay at the end of the
working day?
|
|
|
2.
|
Apply the distributive property to simplify (5x2 +
10y2)2.
|
|
|
3.
|
If shaded tiles are positive and white tiles are negative, use algebra tiles to
represent the product that is represented by the algebra tiles below. 
|
|
|
4.
|
a) Determine an equation for the line with slope –3 and passing
through the origin.
b) What is an equation for the line perpendicular to the line in part
a) that also passes through the origin?
|
|
|
5.
|
Solve this linear system using the method of substitution. 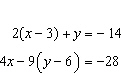
|
Problem
|
|
|
1.
|
Jacob is standing at the top of a ladder. The ladder is 3 m long. It is propped
against a tree, and makes an angle of 74° with the ground. To check his aim, Jacob is tossing
balls into a basket located 4.3 m from the base of the ladder, on the opposite side of the
tree.
a) Determine the distance of the base of the ladder from the tree, in
metres.
b) If Jacob’s eyes are even with the top of the ladder and he looks down on
the bottom of the basket, what is the angle of depression? Answer to the nearest degree.
|
|
|
Use the following information to answer the next two
questions.
The string on Liam’s kite is 42 m long and makes an angle of 70°
with the ground. Liam’s friend, Lucas, is standing directly below the kite.
|
|
|
2.
|
Liam runs away from Lucas, so that the angle of elevation between Lucas and the
kite is 11°. How far apart are Liam and Lucas, to the nearest tenth of a metre?
|
|
|
3.
|
Elizabeth is a doctor who needs to determine when she can administer a second
dose of a particular drug to her patient. She can model the concentration of the drug in the
patient’s bloodstream using the formula C = 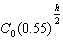 , where •
C is an estimate of the remaining concentration of the drug in the bloodstream, in milligrams
per litre of blood, • C0 is the initial concentration of the dose given,
and • h is the time, in hours, since the dose was administered. How long will it
take for a concentration of 117 mg/L to be reduced to 11 mg/L remaining in the bloodstream? Express
the answer to the nearest hour.
|
|
|
4.
|
A rectangular prism has a width of x cm. Its length is 4 cm more than its
width, and its height is 6 cm more than its length. Write an algebraic expression, in simplified
form, for the volume of the prism 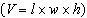 .
|