Name: 
 

Math 10F LG 20 Practice Final #2


Multiple Choice
Identify the choice that best completes the statement or answers the question.
 

 1. 
Which description about the number 225 is correct?
a.
perfect cube
b.
perfect square
c.
both a perfect cube and a perfect square
d.
neither a perfect cube nor a perfect square
 

 2. 
Express 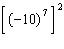mc002-1.jpgas a power with a single exponent.
a.
mc002-2.jpg
b.
mc002-3.jpg
c.
(–10)14
d.
mc002-4.jpg
 

 3. 
Which power is equivalent to 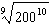mc003-1.jpg?
a.
mc003-2.jpg
b.
mc003-3.jpg
c.
mc003-4.jpg
d.
mc003-5.jpg
 

 4. 
What is the value of x in the equation 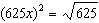mc004-1.jpg?
a.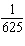
mc004-2.jpg
b.
1
c.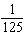
mc004-3.jpg
d.
2
 

 5. 
Which of the following is equivalent to 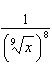mc005-1.jpg?
a.
mc005-2.jpg
b.
mc005-3.jpg
c.
mc005-4.jpg
d.
mc005-5.jpg
 

 6. 
Express 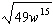mc006-1.jpg as a power with a rational exponent.
a.
mc006-2.jpg
b.
mc006-3.jpg
c.
mc006-4.jpg
d.
mc006-5.jpg
 

 7. 
The expression –12x2 – 36x written in fully factored form is
a.
–12(x2 + 3x)
b.
–12(x2 – 3x)
c.
–12x(x + 3)
d.
–6x(2x + 6)
 

 8. 
The expression –65x2 – 10x + 10 written in factored form is
a.
–5(13x2 + 2x – 2)
b.
–5(–13x2 – 2x + 2)
c.
–5(–13x2 + 2x – 2)
d.
–5(13x2 – 2x + 2)
 

 9. 
Suppose the area of a rectangle is represented by the expression 100x2 – 49. When the expression is fully factored, the factors represent the dimensions of the rectangle. What expressions represent the dimensions of the rectangle?
a.
10x + 7 and 10x – 7
b.
10x + 7 and 10x + 7
c.
10 and 10x2 – 49
d.
10x – 7 and 10x – 7
 

 10. 
What expression is equivalent to x2 – 12x + 36?
a.
(x + 6)(x + 6)
b.
(x – 6)2
c.
(x – 6)(x + 6)
d.
(x + 6)2
 

 11. 
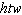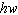What is the least common multiple of the terms mc011-1.jpg, mc011-2.jpg, and mc011-3.jpg?
a.
mc011-4.jpg
b.
mc011-5.jpg
c.
mc011-6.jpg
d.
mc011-7.jpg
 

 12. 
Which pair of integers has a product of –60 and a sum of 4?
a.
–6 and 10
b.
–6 and –10
c.
6 and 10
d.
6 and –10
 

 13. 
Which statement describes what is happening to the skier as she moves from point C to D on the graph?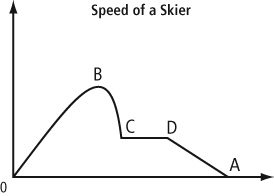

mc013-1.jpg
a.
The skier is increasing speed at a constant rate.
b.
The skier is slowing down and has stopped.
c.
The skier is travelling at a constant speed.
d.
The skier has reached her maximum speed.
 

 14. 
Which of the following tables of values represent(s) a linear relation?

A
x
1
2
4
5
y
9
13
21
25

B
x
1
2
4
5
y
1
4
16
25

C
x
1
2
4
5
y
2
3
4
5

D
x
1
2
4
5
y
10
15
25
30


a.
C
b.
None of the above.
c.
B
d.
A and D
 

 15. 
The cost of a taxi ride is $6.00 plus $0.25 for every 0.5 km. Which graph represents this relation?
a.

mc015-1.jpg
b.

mc015-2.jpg
c.

mc015-3.jpg
d.

mc015-4.jpg
 

 16. 
State the domain of this function in set notation.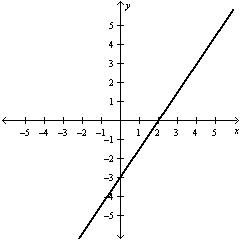

mc016-1.jpg
a.
mc016-2.jpg
b.
mc016-3.jpg
c.
mc016-4.jpg
d.
mc016-5.jpg
 

 17. 
Use the table of values to determine the slope of the relation.


x
y
–6
–1
–8
2
–10
5
–12
8
–14
11
–16
14

a.
mc017-1.jpg
b.
mc017-2.jpg
c.
mc017-3.jpg
d.
mc017-4.jpg
 

 18. 
Which of the following line segment(s) have a zero slope?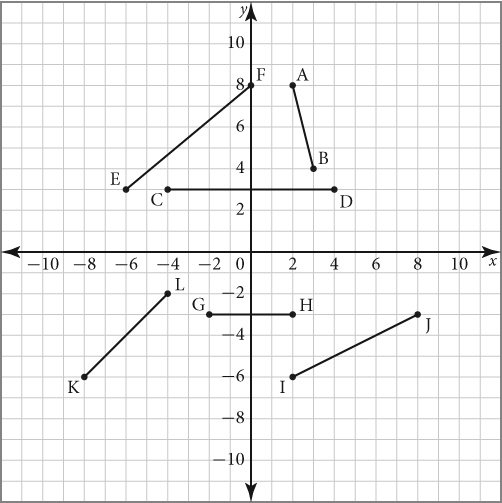

mc018-1.jpg
a.
Line segments IJ, GH, and KL
b.
Line segments CD and GH
c.
Line segments EF, KL, and IJ
d.
Line segment AB
 

 19. 
What is the equation 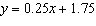mc019-1.jpg in general form?
a.
mc019-2.jpg
b.
mc019-3.jpg
c.
mc019-4.jpg
d.
mc019-5.jpg
 

 20. 
Rewrite the equation 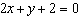mc020-1.jpg in slope-intercept form.
a.
mc020-2.jpg
b.
mc020-3.jpg
c.
mc020-4.jpg
d.
mc020-5.jpg
 

 21. 
Rewrite the equation 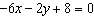mc021-1.jpg in slope-intercept form.
a.
mc021-2.jpg
b.
mc021-3.jpg
c.
mc021-4.jpg
d.
mc021-5.jpg
 

 22. 
Points A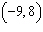mc022-1.jpgand B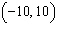mc022-2.jpg are on a line with a y-intercept –10. What is the equation of the line?
a.
mc022-3.jpg
b.
mc022-4.jpg
c.
mc022-5.jpg
d.
mc022-6.jpg
 

 23. 
The equation of the line through the point 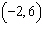mc023-1.jpg with slope –8 is
a.
mc023-2.jpg
b.
mc023-3.jpg
c.
mc023-4.jpg
d.
mc023-5.jpg
 

 24. 
Using the table of values, determine the equation of the line.

x
y
0
–3
–3
24
–6
51
–9
78
–12
105

a.
mc024-1.jpg
b.
mc024-2.jpg
c.
mc024-3.jpg
d.
mc024-4.jpg
 

 25. 
Determine the ordered pair that solves the linear system 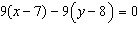mc025-1.jpg and 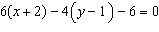mc025-2.jpg.      
a.
mc025-3.jpg
b.
mc025-4.jpg
c.
mc025-5.jpg
d.
mc025-6.jpg
 
 
Answer the following questions using the information from the scenario below.

FunNGames Video rents game machines for $16 and video games for $3 each. Big Vid rents game machines for $12 and video games for $4 each. Let y represent the total rental cost, in dollars, and let x represent the number of games rented.
 

 26. 
What are the coordinates of the solution?
a.
mc026-1.jpg
b.
mc026-2.jpg
c.
mc026-3.jpg
d.
mc026-4.jpg
 

 27. 
Using the substitution method, the solution to the linear system y = –x – 14 and –x + y = 24 is
a.
(0, –14)
b.
(–19, 5)
c.
(–14, 10)
d.
(5, –19)
 

 28. 
Determine the solution to the linear system y = 3x – 13 and y = 5x – 19.
a.
(–3, –4)
b.
(–4, 3)
c.
(3, 4)
d.
(3, –4)
 

 29. 
What is the solution to the linear system 10x – 5y = 125 and –10x – 9y = –55? Use the elimination method.
a.
(–10, –5)
b.
(–10, 5)
c.
(10, –5)
d.
(10, 5)
 

 30. 
Evaluate 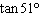mc030-1.jpg, to four decimal places.
a.
0.6293
b.
0.7771
c.
0.7273
d.
1.2349
 

 31. 
In 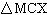mc031-1.jpg, MC = 5 cm and CX = 12 cm. Determine the tangent ratio of 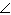mc031-2.jpgX, to the nearest thousandth.

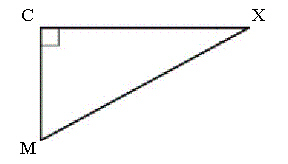mc031-3.jpg
a.
2.400
b.
0.923
c.
0.417
d.
2.600
 

 32. 
In the triangle, QA = 15 cm and tan R = 1.071. What is the length of the hypotenuse, to the nearest tenth of a centimetre?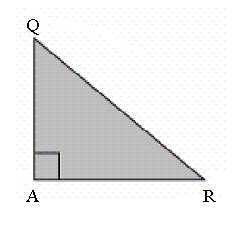
mc032-1.jpg
a.
29.0 cm
b.
15.0 cm
c.
14.0 cm
d.
20.5 cm
 

 33. 
In 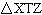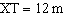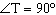mc033-1.jpg, mc033-2.jpg, mc033-3.jpg, and 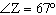mc033-4.jpg. Determine the length of TZ, to the nearest metre.
a.
28 m
b.
5 m
c.
13 m
d.
31 m
 

 34. 
A wheelchair ramp is being built for the entrance to a school. If the ramp makes an angle of 4° with the ground and has a horizontal length of 7 m, determine the height of the ramp, to the nearest tenth of a metre.
a.
0.5 m
b.
7.0 m
c.
1.0 m
d.
4.9 m
 

 35. 
Which statement is incorrect?
a.
You can solve for the unknown side in any triangle, if you know the lengths of the other two sides, by using the Pythagorean theorem.
b.
The hypotenuse is the longest side in a right triangle.
c.
The Pythagorean theorem applies to all right triangles.
d.
The hypotenuse is always opposite the 90° angle in a right triangle.
 

 36. 
Brian mows lawns in the neighborhood and earns $19.00 per lawn. This week he mows 4 lawns and also receives $120 during a birthday party. Brian decides to use a maximum of 40% of his income as spending money. What is the maximum amount of spending money he has for the week?
a.
$117.60
b.
$55.60
c.
$30.40
d.
$78.40
 

 37. 
Quon works as a hotel greeter in the summer earning $11.75/h. During the week he works the following hours earns the following in tips:

Monday: 10 h plus $22 in tips
Tuesday: 0 h plus $0 in tips
Wednesday: 9 h plus $46 in tips
Thursday: 7 h plus $44 in tips
Friday: 11 h plus $8  in tips
Saturday: 0 h plus $0 in tips
Sunday: 0 h plus $0 in tips

What is his gross pay for the week?
a.
$434.75
b.
$554.75
c.
$591.75
d.
$314.75
 

 38. 
Mirka receives a pay stub from she job as an athletic trainer. She is paid weekly.

Earnings Statement
Employee Name: Smith, Mirka
Occupation: Executive Assistant
Period End Date: March 20
Cheque Number: 1274

Earnings    Deductions 
DescriptionHoursRateAmount DescriptionAmount
Regular Hours4015.25
610.00
 Income Tax
415.94
Overtime1022.88
228.75
 EI
33.01
Overtime1930.50
579.50
 CPP
99.76
Vacation Pay  
56.73
   
Gross Pay  
1474.98
 Total Deductions
548.71
     Net Pay
*****
Due to a computer glitch her Net Pay was not shown. What was Mirka’s net pay for the pay period?
a.
$1966.96
b.
$2023.69
c.
$926.27
d.
$1097.43
 
 
Use the pay stub to answer the following questions.

Hunter receives a pay stub from his job as an executive assistant. He is paid weekly. Due to a computer glitch some of the calculations were replaced by “ *****”.

Earnings Statement
Employee Name: Smith, Hunter
Occupation: Writer/Editor
Period End Date: March 20
Cheque Number: 1285

Earnings    Deductions 
DescriptionHoursRate
Amount
 Description
Amount
Regular Hours4019.75
*****
 Income Tax
203.99
Overtime2.529.63
*****
 EI
14.92
Overtime039.50
*****
 CPP
44.48
Vacation Pay  
34.56
   
Gross Pay  
*****
 Total Deductions
*****
     Net Pay
*****
 

 39. 
How much money did Hunter earn at his regular rate of pay?
a.
$29.63
b.
$898.64
c.
$790.00
d.
$39.50
 

 40. 
How much money was deducted from Hunter’s pay cheque for the pay period?
a.
$297.95
b.
$248.47
c.
$174.43
d.
$263.39
 

Short Answer
 

 1. 
Brian works as a realtor and earns 3.50% commission on a home sale of $767 473. How much money did he make on the sale?
 

 2. 
Quon is hired as a data entry clerk and earns $25.00/h with a 7.75 h work day. The position is unionized with 1.00% deducted for union dues. In addition,  income tax of $29.06, CPP contributions of $9.59, and EI of $3.22. What is Quon’s net pay at the end of the working day?
 

 3. 
Evaluate 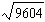sa003-1.jpg using prime factorization.
 

 4. 
Points 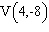sa004-1.jpg and 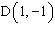sa004-2.jpg are on a line. Determine the slope of the line.
 

 5. 
Determine the number of solutions for the following linear system by using a graph.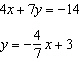
sa005-1.jpg
sa005-2.jpg
 

Problem
 

 1. 
A wheelchair ramp has a height of 0.5 m and a horizontal length of 5 m. Determine the angle that the ramp makes with the ground, to the nearest degree.
 

 2. 
Olivia was asked to simplify an expression involving powers. Her solution is shown.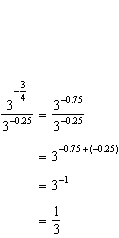
pr002-1.jpg
a) Identify the error that Olivia made.
b) Give the correct solution.
 

 3. 
A rectangular prism has a width of x cm. Its length is 4 cm more than its width, and its height is 6 cm more than its length. Write an algebraic expression, in simplified form, for the volume of the prism 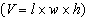pr003-1.jpg.
 

 4. 
Two angles sum to 90 degrees. One angle is 32 degrees larger than than the other. What are the two angles?
 



 
Check Your Work     Start Over