Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Evaluate 0.0013.
a. | 0.001 | b. | 0.000001 | c. | 0 | d. | 0.000000001 |
|
|
|
2.
|
Determine the cube root of 216s3.
|
|
|
3.
|
Express 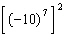 as a power with a single exponent.
|
|
|
4.
|
Carbon-14 is a radioactive element with a half-life of 5700 years. If a sample
contains 16 g of carbon-14 today, what mass of carbon-14 will it contain in 45 600 years? 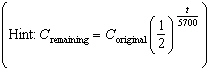 a. | 4 g | b. | 0.0625 g | c. | 2–45
600 g | d. | 32 g |
|
|
|
5.
|
Which power is equivalent to 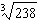 ?
|
|
|
6.
|
Express 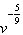 as an equivalent radical.
|
|
|
7.
|
Rhada’s bedroom floor has a width equal to 10x + 5 and a length
equal to 5x – 7. What equation represents the area of the floor?
a. | A = 50x2 + 95x – 35 | b. | A =
50x2 + 45x – 35 | c. | A = 50x2 –
95x – 35 | d. | A = 50x2 –
45x – 35 |
|
|
|
8.
|
The area of a rectangular picture frame is represented by the equation A
= 14x2 – 35x. When the expression is factored fully, the factors are
the dimensions of the frame. What are the dimensions of the frame?
a. | 7x by 2x – 5 | b. | 7x2 by 2x –
5 | c. | 7 by 2x2 – 5 | d. | 7 by 2x –
5 |
|
|
|
9.
|
The area, in square metres, of Jack’s driveway is represented by the
expression 64x2. Jack shovelled 100 m2 of the driveway before taking a
break. Suppose the remaining area of the driveway is rectangular. What are the dimensions of the
rectangle?
a. | 8x + 10 by 8x – 10 | b. | 10 – 8x by 10 –
8x | c. | 8x – 10 by 8x – 10 | d. | 10 + 8x by 10
– 8x |
|
|
|
10.
|
Identify the pair of integers that has a product of –24 and a sum of
10.
a. | 12 and –2 | b. | –12 and –2 | c. | –12 and
2 | d. | 12 and 2 |
|
|
|
11.
|
What is the factored form of 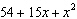 ?
|
|
|
12.
|
Which multiplication statement is represented by the algebra tiles
below? 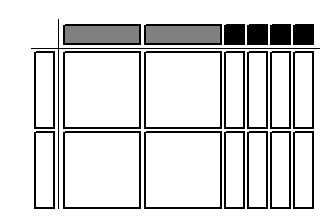
|
|
|
13.
|
Which of the following tables of values represent(s) a linear
relation?
a. | C | b. | None of the above. | c. | B | d. | A and D |
|
|
|
14.
|
Which of the following tables of values represent(s) a linear
relation?
a. | A and D | b. | C | c. | B | d. | None of the
above. |
|
|
|
15.
|
Use set notation to state the domain of this function. 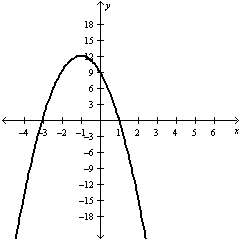
|
|
|
16.
|
Which relation is a function?
a. | {(3, 4), (9, 8), (3, 5), (1, 3)} | b. | {(1, 2), (4, 7), (8, 9), (3,
3)} | c. | {(9, 0), (1, 2), (1, 4), (4, 2)} | d. | {(2, 1), (2, 4), (5, 9), (1,
16)} |
|
|
|
17.
|
Evaluate 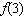 for the function 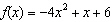 .
|
|
|
18.
|
Use the table of values to determine the slope of the relation.
x | y | –6 | –1 | –8 | 2 | –10 | 5 | –12 | 8 | –14 | 11 | –16 | 14 | | |
|
|
|
19.
|
The y-intercept of the line 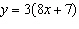 is
|
|
|
20.
|
Amelia invested $600 in an account that pays 10% simple interest per year. The
equation representing Amelia’s investment is A = P + Prt, where A
is the value of the investment, in dollars, P is the starting principle amount, in dollars,
r is the interest rate written as a decimal, and t is the number of years the money is
invested. How many years will pass before the investment is worth $3000?
|
|
|
21.
|
Elizabeth invested $500 in an account that pays 5% simple interest per year. The
equation representing Elizabeth’s investment is A = P + Prt, where
A is the value of the investment, in dollars, P is the starting principle amount, in
dollars, r is the interest rate written as a decimal, and t is the number of years the
money is invested. What is the value of the investment after 40 years?
a. | $1000 | b. | $10500 | c. | $1500 | d. | $100500 |
|
|
|
22.
|
What is the slope of the line with an x-intercept of 8 and a
y-intercept of –5?
|
|
|
23.
|
Using the table of values, determine the equation of the line.
|
|
|
24.
|
What is the equation of the line that passes through 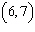 and is perpendicular to
the line 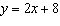 ?
|
|
|
25.
|
Translate the following sentence into an equation: “Seven less than two
times a number is nine less than two times the number.”
|
|
|
Answer the following questions using the information from the scenario
below.
Globo-Gym charges a flat fee of $20 per month plus $4.00 per visit. Average
Joe’s charges a flat fee of $30 per month plus $2.00 per visit. Let x represent the
number of visits per month and let y represent the total cost per month, in dollars.
|
|
|
26.
|
Which statement best describes what the solution to this linear system
represents?
a. | When 40 gym visits are made at either fitness centre, the cost is
$5. | b. | It costs more to be a member at Globo-Gym. | c. | When 5 gym visits
are made at either fitness centre, the cost is $40. | d. | It costs more to be a member at Average
Joe’s. |
|
|
|
27.
|
Daniel has a large collection of basketball cards. He estimates that he has
spent $174.00 on protective card holders and an average of $8.50 on each card. If he sells his cards
at $23 each, how much money will he have made when his costs equal his revenue?
a. | $174.00 | b. | $14.50 | c. | $276.00 | d. | $12 |
|
|
|
28.
|
Dylan’s widget company has constant costs of $390 every month, plus $20
per widget, w, manufactured. He sells each widget for $30. A system of equations to represent
Dylan’s expenses and revenue is
C = 390 + 20w
C = 30w
How
many widgets must Dylan sell every month for his costs to equal his revenue?
|
|
|
29.
|
Emily babysits for a fee of $34.50 for one evening plus $1.15 per diaper change.
Cindy charges $27.60 for one evening plus $2.30 per diaper change. How many diapers does each girl
have to change in order to charge the same total fee?
|
|
|
30.
|
In the triangle, QA = 15 cm and tan R = 1.071. What is the length of the
hypotenuse, to the nearest tenth of a centimetre? 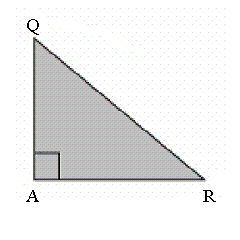 a. | 29.0 cm | b. | 15.0 cm | c. | 14.0
cm | d. | 20.5 cm |
|
|
|
31.
|
A surveyor, S, is measuring the width of a street, using a marker, M. The
surveyor cannot measure the width directly, because there is too much traffic. She stands on the east
side of the intersection. The marker is on the west side of the intersection, and is 18 m north of
the intersection. Determine the width of the street, to the nearest tenth of a
metre. 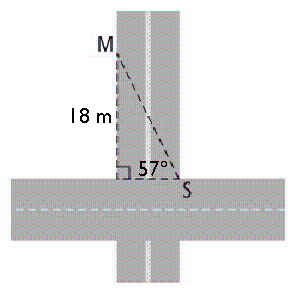 a. | 33.0 m | b. | 21.5 m | c. | 11.7
m | d. | 27.7 m |
|
|
|
32.
|
A motorized wheelchair ramp is being built for the entrance to a school. If the
ramp makes an angle of 6° with the ground and has a horizontal length of 9 m, determine the
length of the ramp, to the nearest hundredth of a metre.
a. | 0.95 m | b. | 9.51 m | c. | 0.86
m | d. | 9.05 m |
|
|
|
33.
|
A ladder leans against a vertical wall and makes an angle of 80.7° with the
ground. The foot of the ladder is 1.5 m from the base of the wall. Determine the length of the
ladder, to the nearest tenth of a metre.
a. | 9.1 m | b. | 9.3 m | c. | 9.2
m | d. | 1.5 m |
|
|
|
34.
|
A ladder leans against a vertical wall and makes an angle of 60° with the
ground. The top of the ladder is 4.9 m from the base of the wall. Determine the horizontal distance
from the base of the wall to the bottom of the ladder, to the nearest tenth of a metre.
a. | 2.8 m | b. | 1.4 m | c. | 5.6
m | d. | 2.4 m |
|
|
|
35.
|
In 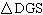 , GS = 63 cm and sin D = 0.88. Determine the length of DG,
to the nearest centimetre.
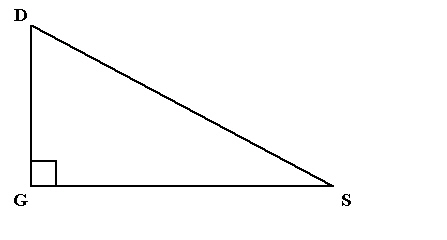 a. | 34 cm | b. | 72 cm | c. | 55
cm | d. | 81 cm |
|
|
|
36.
|
Cheng does odd jobs for his family and the neighbours. He keeps track of the
jobs he does on his block for the week and records them in the chart below: | Job | Hourly Pay | | Babysitting | $11.50 | | Dog Walking | $6.00 | | Car Wash | $7.50 | | Gardening | $12.00 | | Mowing Lawns | $10.50 | | |
If Cheng babysits for 4 h, walks dogs for 2 h, washes cars for 1 h,
gardens for 4 h and mows lawns for 5 h what is his income for the week. a. | $166.00 | b. | $140.50 | c. | $161.00 | d. | $142.00 |
|
|
|
37.
|
Cai earns an annual salary of $73 000. Her total deductions for the year are $14
965.00, $5621.00, $2593.80, and $858.22 for federal tax, provincial tax, CPP, and EI, respectively
each year. What were Cai’s total deductions for the year?
a. | $24 038.02 | b. | $78 891.98 | c. | $48
961.98 | d. | $73 000.00 |
|
|
|
38.
|
Mirka receives a pay stub from she job as an athletic trainer. She is paid
weekly. Earnings Statement Employee Name: Smith, Mirka Occupation: Executive
Assistant Period End Date: March 20 Cheque Number: 1274 | Earnings | | | | | Deductions | | | Description | Hours | Rate | Amount | | Description | Amount | | Regular Hours | 40 | 15.25 | 610.00 | | Income Tax | 415.94 | | Overtime | 10 | 22.88 | 228.75 | | EI | 33.01 | | Overtime | 19 | 30.50 | 579.50 | | CPP | 99.76 | | Vacation
Pay | | | 56.73 | | | | | Gross Pay | | | 1474.98 | | Total Deductions | 548.71 | | | | | | | Net
Pay | ***** | | | | | | | |
Due to a
computer glitch her Net Pay was not shown. What was Mirka’s net pay for the pay
period? a. | $1966.96 | b. | $2023.69 | c. | $926.27 | d. | $1097.43 |
|
|
|
Use the pay stub to answer the following questions.
Hunter
receives a pay stub from his job as an executive assistant. He is paid weekly. Due to a computer
glitch some of the calculations were replaced by “ *****”. Earnings
Statement Employee Name: Smith, Hunter Occupation: Writer/Editor Period End Date: March
20 Cheque Number: 1285 | Earnings | | | | | Deductions | | | Description | Hours | Rate | Amount | | Description | Amount | | Regular
Hours | 40 | 19.75 | ***** | | Income Tax | 203.99 | | Overtime | 2.5 | 29.63 | ***** | | EI | 14.92 | | Overtime | 0 | 39.50 | ***** | | CPP | 44.48 | | Vacation
Pay | | | 34.56 | | | | | Gross Pay | | | ***** | | Total Deductions | ***** | | | | | | | Net
Pay | ***** | | | | | | | |
|
|
|
39.
|
How much money did Hunter earn at his regular rate of pay?
a. | $29.63 | b. | $898.64 | c. | $790.00 | d. | $39.50 |
|
|
|
40.
|
Ali is hired by the Ministry of Forests plant trees for the summer. On average
he plants 3500 trees per week. What is Ali’s gross pay at the end of the 6 weeks if he is paid
$0.17 per tree?
a. | $3570.00 | b. | $357.00 | c. | $5950.00 | d. | $595.00 |
|
Short Answer
|
|
|
1.
|
Evaluate 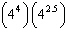 using a calculator. Express the answer to four decimal
places, where necessary.
|
|
|
2.
|
Factor the trinomial 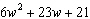 .
|
|
|
3.
|
a) Explain how graphing can be used to solve a linear system of two
equations.
b) Explain how you could check your solution.
|
|
|
4.
|
Express each statement as an algebraic equation.
a) One sixth of a
number, increased by seven, is 47.
b) Five times a number, subtracted from seven, is five
less than twice the number.
c) When tickets to a play cost $5 each, the revenue at the box
office is $230.
d) The sum of the length and width of a backyard pool is 98 m.
|
|
|
5.
|
Predict the number of solutions for the system of equations. Justify your
answer. 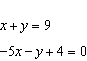
|
Problem
|
|
|
1.
|
Emily is printing T-shirts for a school fundraiser. There is a cost of $18 to
set up the printing. Each T-shirt costs $5 to produce. If the school charges $8 for each shirt, how
many T-shirts must Emily print in order for the school to break even?
|
|
|
2.
|
EZ Online Digital Photos charges $0.15 per digital photo and a flat rate of
$3.25 per order. The local pharmacy charges $0.28 per digital photo. Under what conditions is the
cost to print the digital photos the same for either store?
|
|
|
3.
|
One metal alloy is 12% silver, while another is 37% silver. How much of each
alloy should be used to make 1500 g of a metal alloy that is 25% silver?
|
|
|
4.
|
Two angles sum to 90 degrees. One angle is 32 degrees larger than than the
other. What are the two angles?
|