Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
What is the volume of a cube with edges of length 7 m?
a. | 1029 m3 | b. | 343 m3 | c. | 49
m3 | d. | 294 m3 |
|
|
|
2.
|
Which description about the number 225 is correct?
a. | perfect cube | b. | perfect square | c. | both a perfect cube
and a perfect square | d. | neither a perfect cube nor a perfect
square |
|
|
|
3.
|
Which value of x satisfies the equation 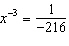 ?
|
|
|
4.
|
Determine the value of y in the equation y = 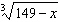 when x
= 122. Leave your answer in simplest radical form if necessary.
|
|
|
5.
|
Express 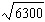 as an equivalent mixed radical.
|
|
|
6.
|
Which expression has the largest value?
|
|
|
7.
|
Rhada’s bedroom floor has a width equal to 10x + 5 and a length
equal to 5x – 7. What equation represents the area of the floor?
a. | A = 50x2 + 95x – 35 | b. | A =
50x2 + 45x – 35 | c. | A = 50x2 –
95x – 35 | d. | A = 50x2 –
45x – 35 |
|
|
|
8.
|
What value of k makes the trinomial 36x2 + kx +
81 a perfect square?
|
|
|
9.
|
What expression is equivalent to x2 – 12x +
36?
a. | (x + 6)(x + 6) | b. | (x –
6)2 | c. | (x – 6)(x + 6) | d. | (x +
6)2 |
|
|
|
10.
|
What is the least common multiple of the terms 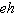 , 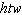 , and
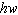 ?
|
|
|
11.
|
Which multiplication statement is represented by the algebra tiles
below? 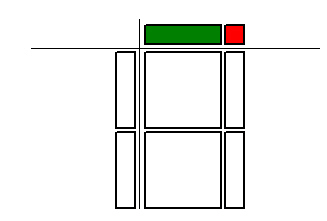
|
|
|
12.
|
Which multiplication statement is represented by the algebra tiles
below? 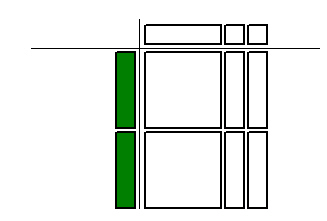
|
|
|
13.
|
Use set notation to state the range of this function. 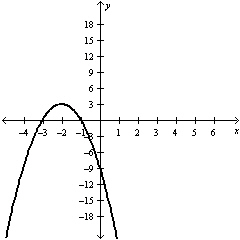
|
|
|
14.
|
Use set notation to state the range of this function. 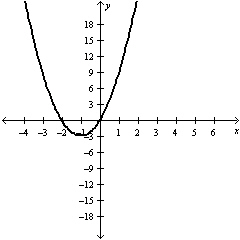
|
|
|
15.
|
Which of the following represents the range of the relation 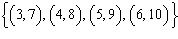 ?
|
|
|
16.
|
Points 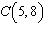 and 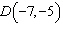 are on a line. What is the run from point
D to point C?
|
|
|
17.
|
The rate of change of a horizontal line is
a. | positive | b. | negative | c. | undefined | d. | zero |
|
|
|
18.
|
Which of the following line segment(s) have a zero slope? 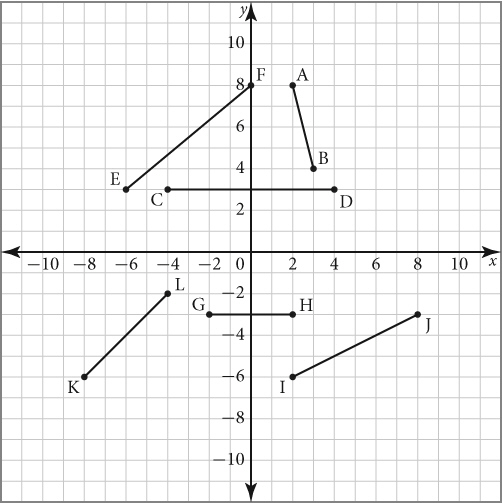 a. | Line segments IJ, GH, and KL | b. | Line segments CD and GH | c. | Line segments EF,
KL, and IJ | d. | Line segment AB |
|
|
|
19.
|
Amelia invested $600 in an account that pays 10% simple interest per year. The
equation representing Amelia’s investment is A = P + Prt, where A
is the value of the investment, in dollars, P is the starting principle amount, in dollars,
r is the interest rate written as a decimal, and t is the number of years the money is
invested. How many years will pass before the investment is worth $3000?
|
|
|
20.
|
Rewrite the equation 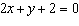 in slope-intercept form.
|
|
|
21.
|
Identify the y-intercept of the relation represented by the equation 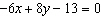 .
|
|
|
22.
|
Points C 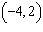 and D 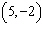 are on a line. What is the run from point
C to D?
|
|
|
23.
|
The equation of line A is 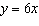 . The equation of line B is
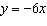 . The equation of line C is 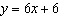 . The equation of line D is 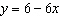 . Which lines are parallel to line A? a. | line C | b. | line C and line D | c. | line B and line
D | d. | line B |
|
|
|
24.
|
Points G 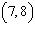 and H 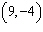 are on a line. Which equation represents
a line that is parallel to this line?
|
|
|
Answer the following questions using the information from the scenario
below.
Ava is looking at banquet halls for her parents’ anniversary party. Moonlight
Hall charges a fixed cost of $1100 plus $75 per guest. Riverside Hall charges $950 plus $100 per
guest. Let C represent the total cost, in dollars, and let n represent the number of
guests.
|
|
|
25.
|
Identify the system of linear equations that represents this situation.
a. | Moonlight: C = 1100 – 75n
Riverside: C = 950 –
100n | b. | Moonlight: C = 100n + 950
Riverside: C = 75n +
1100
| c. | Moonlight: C = 75n + 1100
Riverside: C = 100n +
950
| d. | Moonlight: C = 1100n + 75
Riverside: C = 950n +
100 |
|
|
|
26.
|
Which of the following pairs of linear equations represents coincident
lines?
|
|
|
27.
|
What is the x-coordinate at the point of intersecton for the the linear
system 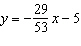 and 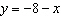 ?
|
|
|
28.
|
The perimeter of a rectangle is 58 m. The length is 4 m less than twice the
width. What is the length of the rectangle?
|
|
|
29.
|
The total number of known moons around Planet X, Planet Y, and Planet Z. The
total number of moons around Planet X and Planet Y is 4 more than the number of moons around Planet
Z. Planet X has 3 moons more than twice the number of moons around Planet Y. How many moons does each
planet have?
a. | Planet X has 43 moons, Planet Y has 59 moons, and Planet Z has 20
moons. | b. | Planet X has 59 moons, Planet Y has 43 moons, and Planet Z has 20
moons. | c. | Planet X has 20 moons, Planet Y has 43 moons, and Planet Z has 59
moons. | d. | Planet X has 43 moons, Planet Y has 20 moons, and Planet Z has 59
moons. |
|
|
|
30.
|
In the triangle, QA = 15 cm and tan R = 1.071. What is the length of the
hypotenuse, to the nearest tenth of a centimetre? 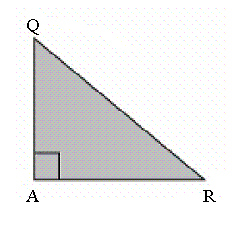 a. | 29.0 cm | b. | 15.0 cm | c. | 14.0
cm | d. | 20.5 cm |
|
|
|
31.
|
A wheelchair ramp is being built for the entrance to a school. If the ramp makes
an angle of 3.9° with the ground and has a vertical height of 0.58 m, determine the horizontal
length of the ramp, to the nearest tenth of a metre.
a. | 8.5 m | b. | 5.8 m | c. | 1.2
m | d. | 0.9 m |
|
|
|
32.
|
A ladder leans against a vertical wall and makes an angle of 80.7° with the
ground. The foot of the ladder is 1.5 m from the base of the wall. Determine the length of the
ladder, to the nearest tenth of a metre.
a. | 9.1 m | b. | 9.3 m | c. | 9.2
m | d. | 1.5 m |
|
|
|
33.
|
What is the sine ratio of 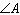 ? ?
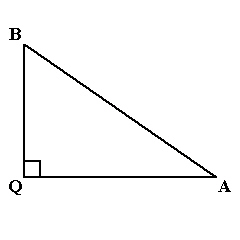
|
|
|
34.
|
What is the value of sin 0°?
|
|
|
35.
|
Determine the measure of 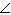 J, to the nearest degree. 
|
|
|
36.
|
On a recent 4.75-h shift a DJ earns $11.45/h plus $39.75 in tips. If 30% is
deducted and transferred to a savings account to be saved towards a school trip how much money will
she save from the shift?
a. | $24.81 | b. | $28.24 | c. | $16.79 | d. | $25.67 |
|
|
|
37.
|
The Canada Pension Plan (CPP) rate is currently 4.95% of a person’s gross
pay up to a maximum of $2593.80. If the government were to change the rate to 3.13%, what would be
the difference in CPP payments for an annual salary of $40 000?
a. | $728.00 less than the original rate | b. | $691.60 more than the original
rate | c. | $728.00 more than the original rate | d. | $764.40 less than the original
rate |
|
|
|
38.
|
Erek worked 40 h at $17.00/h. He has deductions totalling $146.95. What was
Erek’s net pay?
a. | $386.10 | b. | $680.00 | c. | $203.95 | d. | $533.05 |
|
|
|
39.
|
Lucas receives a pay stub from his job as an executive assistant. He is paid
bi-weekly. Earnings Statement Employee Name: Wong, Lucas Occupation: Athletic
Trainer Period End Date: June 18 Cheque Number: 1317 | Earnings | | | | | Deductions | | | Description | Hours | Rate | Amount | | Description | Amount | | Regular
Hours | 80 | 20.50 | 1640.00 | | Income Tax | 748.02 | | Overtime | 18 | 30.75 | 553.50 | | EI | 21.46 | | Overtime | 0 | 41.00 | 0.00 | | CPP | 64.85 | | Vacation
Pay | | | 87.74 | | | | | Gross Pay | | | 2281.24 | | Total Deductions | 834.33 | | | | | | | Net
Pay | 1446.91 | | | | | | | |
What
is Lucas’s gross pay for the year? a. | $118 624.48 | b. | $54 749.76 | c. | $59
312.24 | d. | $27 374.88 |
|
|
|
Use the pay stub to answer the following questions.
Hunter
receives a pay stub from his job as an executive assistant. He is paid weekly. Due to a computer
glitch some of the calculations were replaced by “ *****”. Earnings
Statement Employee Name: Smith, Hunter Occupation: Writer/Editor Period End Date: March
20 Cheque Number: 1285 | Earnings | | | | | Deductions | | | Description | Hours | Rate | Amount | | Description | Amount | | Regular
Hours | 40 | 19.75 | ***** | | Income Tax | 203.99 | | Overtime | 2.5 | 29.63 | ***** | | EI | 14.92 | | Overtime | 0 | 39.50 | ***** | | CPP | 44.48 | | Vacation
Pay | | | 34.56 | | | | | Gross Pay | | | ***** | | Total Deductions | ***** | | | | | | | Net
Pay | ***** | | | | | | | |
|
|
|
40.
|
How much money did Hunter earn at double time?
a. | $829.50 | b. | $0.00 | c. | $74.08 | d. | $859.13 |
|
Short Answer
|
|
|
1.
|
A telephone pole is secured with a guy wire as shown in the diagram. The guy
wire makes an angle of 72° with the ground and is secured to the ground 9 m from the bottom of
the pole. Determine the height of the telephone pole, to the nearest tenth of a metre. 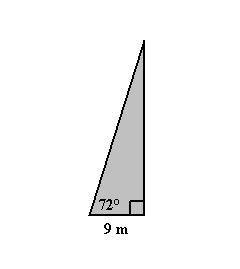
|
|
|
2.
|
Owen decides to go parasailing while on vacation. The flyer advertises that the
maximum height reached during the trip will be 51 m. If the parasailing cable is 92 m long, what
angle will the cable make with the horizontal when Owen reaches the maximum height? Express your
answer to the nearest degree.
|
|
|
3.
|
Write 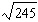 in simplist form.
|
|
|
4.
|
What is the factored form of the trinomial 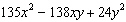 .
|
|
|
5.
|
Supplementary angles are angles that have a sum of 180°. If 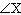 and 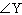 are
supplementary, and 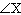 is 44° greater than 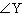 , what are the values of
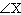 and 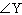 ?
|
Problem
|
|
|
Use this information to answer the following questions.The school
parking lot is rectangular. Its area can be represented by the binomial 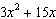 .
|
|
|
1.
|
Identify the greatest common factor (GCF) of the area and write expressions for
the dimensions of the parking lot by fully factoring its area.
|
|
|
Answer the next three questions using the following information:A
flight from Montreal to London is modelled by the graph below.
Flight From Montreal to
London 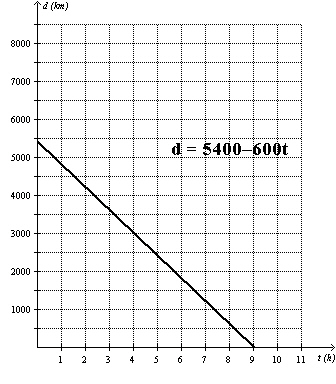
|
|
|
2.
|
What are the domain and range of the relation that models this situation?
|
|
|
3.
|
Sophia needs to mail a package to her grandmother. When she gets it weighed at
the post office, she finds that the postage on the parcel is $1.10. Sophia only has nickels and dimes
with her.
a) If Sophia pays only with nickels, how many would she need?
b)
Identify three different combinations Sophia can use to pay with both nickels and dimes.
c)
Determine the equation of the line relating the number of nickels and dimes to model this
situation.
d) Do not graph this line, but determine the intercepts of the graph. What do
they represent?
|
|
|
4.
|
The distance-time graph shows Emily’s distance from a video camera, where
d represents her distance from the camera, in metres, and t represents time, in
seconds. 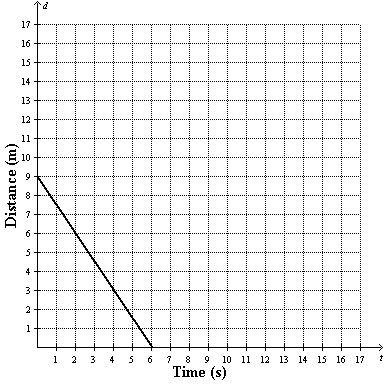 a) a) Identify the d-intercept and
explain what it means. b) Identify the t-intercept and explain what it
means. c) What is the equation of the line, in general form?
|