Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Simplify 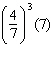 . a. | 448 | b. | 64 | c. | 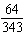 | d. | 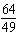 |
|
|
|
2.
|
Which expression represents the volume of a cube of edge length
8k?
|
|
|
3.
|
Carbon-14 is a radioactive element with a half-life of 5700 years. If a sample
contains 16 g of carbon-14 today, what mass of carbon-14 will it contain in 45 600 years? 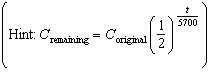 a. | 4 g | b. | 0.0625 g | c. | 2–45
600 g | d. | 32 g |
|
|
|
4.
|
For what value of x do 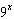 , 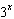 , and 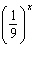 have the same
value? a. | x = 0 | b. | 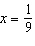 | c. | x =
9 | d. | x = 3 |
|
|
|
5.
|
Which of the following is equivalent to 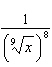 ?
|
|
|
6.
|
Which of the following is equivalent to 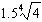 ?
|
|
|
7.
|
Multiply and simplify (7x + 4)2.
a. | 49x2 + 16 | b. | 49x2 + 56x +
16 | c. | 49x2 + 28x + 16 | d. | 49x2 + 56x + 28 |
|
|
|
8.
|
What binomial multiplication expression does the diagram represent? 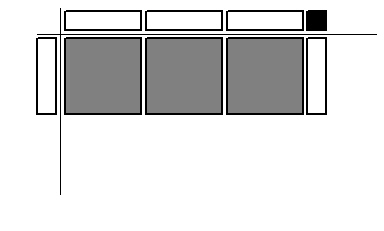
|
|
|
9.
|
What is the factored form of the expression –14x + 14?
a. | –2(7x – 7) | b. | 2(7x + 7) | c. | 2(7x –
7) | d. | –2(7x + 7) |
|
|
|
10.
|
Suppose the area of a rectangle is represented by the expression
100x2 – 49. When the expression is fully factored, the factors represent the
dimensions of the rectangle. What expressions represent the dimensions of the rectangle?
a. | 10x + 7 and 10x – 7 | b. | 10x + 7 and
10x + 7 | c. | 10 and 10x2 – 49 | d. | 10x – 7
and 10x – 7 |
|
|
|
11.
|
What is the factored form of 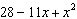 ?
|
|
|
12.
|
Which multiplication statement is represented by the algebra tiles
below? 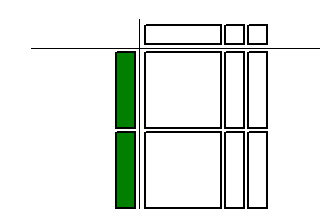
|
|
|
13.
|
How many of the four relations shown below are linear? 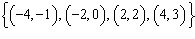
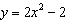 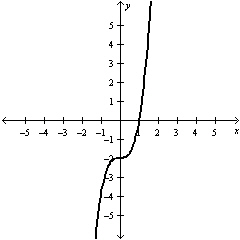 a. | Three of the above | b. | One of the above | c. | None of the
above | d. | Two of the above |
|
|
|
14.
|
State the domain of this function in set notation. 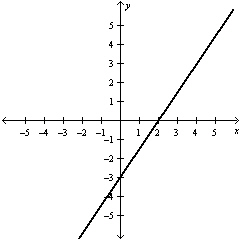
|
|
|
15.
|
Use set notation to state the domain of this function. 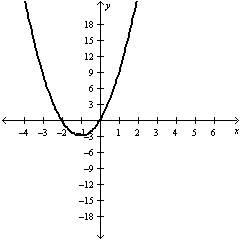
|
|
|
16.
|
Which of the following represents the range of the relation 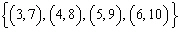 ?
|
|
|
17.
|
Which of the following represents the domain of the relation 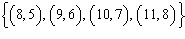 ?
|
|
|
18.
|
Evaluate 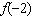 for the function 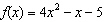 .
|
|
|
19.
|
Identify the equation of the line with a slope of –2 and a
y-intercept of –9.
|
|
|
20.
|
Which equation represents the line containing points C and D? 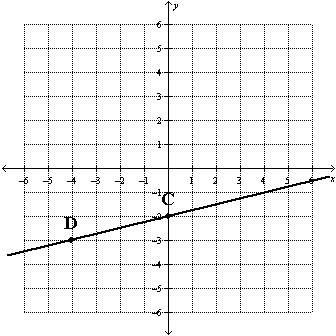
|
|
|
21.
|
A line passes through the point 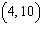 and has a y-intercept of 2. What
is the equation of the line?
|
|
|
22.
|
What is the equation of the line through points 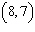 and 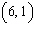 ?
|
|
|
23.
|
Using the table of values, determine the slope of the line.
|
|
|
24.
|
Give the equation of a line that goes through point A and is perpendicular to
the line shown below. 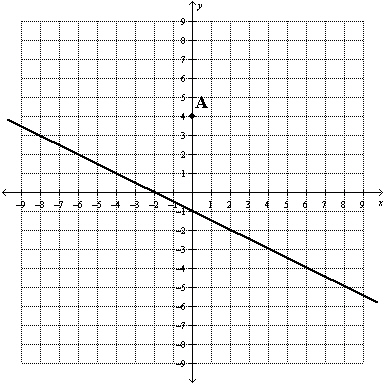
|
|
|
25.
|
What is the equation for the relation 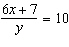 in the form y = mx +
b?
|
|
|
Answer the following questions using the information from the scenario
below.
FunNGames Video rents game machines for $16 and video games for $3 each. Big Vid
rents game machines for $12 and video games for $4 each. Let y represent the total rental
cost, in dollars, and let x represent the number of games rented.
|
|
|
26.
|
Which statement best describes what the point of intersection of this linear
system represents?
a. | When 28 videos are rented at either video store, the cost is $4. | b. | It costs more to
rent games at Big Vid. | c. | When 4 videos are rented at either video store,
the cost is $28. | d. | It costs more to rent games at FunNGames Video. |
|
|
|
27.
|
Use the substitution method to determine the solution to the linear system
y = 4x + 34 and y = –2x – 26.
a. | (–10, –6) | b. | (10, –6) | c. | (–10,
6) | d. | (–6, –10) |
|
|
|
28.
|
What is the y-coordinate of the solution to the linear system 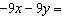
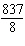 and 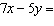 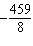 ? a. | 2 | b. | –2 | c. | 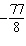 | d. | 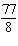 |
|
|
|
29.
|
Mia works at Electronics Plus for $15.00 per day plus $1.80 commission for each
item she sells. Michael works at Techno Gadgets for $18.00 per day plus $1.50 commission for each
item he sells. How many items must each of them sell in order for Mia and Michael to make the same
amount of money in one day?
|
|
|
30.
|
If 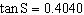 , determine the measure of 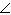 S, to the nearest
degree.
|
|
|
31.
|
If 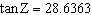 , determine the measure of 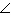 Z, to the nearest
degree.
|
|
|
32.
|
In 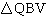 , QV = 9 cm and VB = 12 cm. Determine the
tangent ratio of 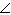 Q, to the nearest thousandth.
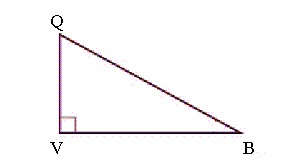 a. | 1.667 | b. | 0.750 | c. | 1.333 | d. | 0.800 |
|
|
|
33.
|
A surveyor, S, is measuring the width of a street, using a marker, M. The
surveyor cannot measure the width directly, because there is too much traffic. She stands on the east
side of the intersection. The marker is on the west side of the intersection, and is 18 m north of
the intersection. Determine the width of the street, to the nearest tenth of a
metre. 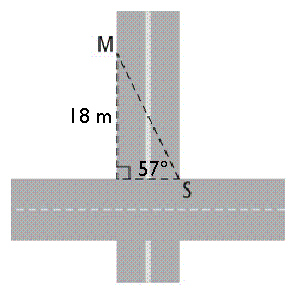 a. | 33.0 m | b. | 21.5 m | c. | 11.7
m | d. | 27.7 m |
|
|
|
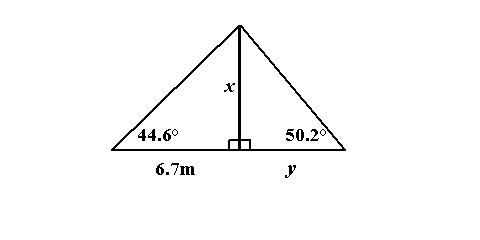
Use the diagram to answer the following question(s).
|
|
|
34.
|
Determine the length of x, to the nearest tenth of a metre.
a. | 6.6 m | b. | 11.2 m | c. | 12.8
m | d. | 5.5 m |
|
|
|
35.
|
If sin A = 0.5592, then the measure of  A, to the nearest degree,
is
|
|
|
36.
|
A truck driver earns $21.75/h and works 7.75 hours. How much money did the truck
driver earn?
a. | $168.56 | b. | $152.25 | c. | $29.50 | d. | $146.81 |
|
|
|
37.
|
A desk clerk works the late shift and earns $236.31 for the 7.25-h shift. A
shift premium of $75.00 is paid for working later. What is the regular rate of pay/h?
a. | $22.25 | b. | $10.34 | c. | $3.15 | d. | $42.94 |
|
|
|
38.
|
Carmen earns an annual salary of $47 000. Her total deductions for the year are
$9635.00, $3619.00, $2326.50, and $780.20 for federal tax, provincial tax, CPP, and EI, respectively
each year. What is Carmen’s net pay for the year?
a. | $30 639.30 | b. | $49 909.30 | c. | $47
000.00 | d. | $16 360.70 |
|
|
|
39.
|
Jacob is hired by the Ministry of Forests to plant trees for the summer. On
average he plants 3300 per week and is paid $0.19 per tree. Jacob has deductions of $144.21, $31.04
and $10.41 taken from his paycheque each week for income tax, CPP, and EI respectively. What
percentage of his income does he take home at the end of 9 weeks?
a. | 70.39% | b. | 92.18% | c. | 62.57% | d. | 29.61% |
|
|
|
Use the pay stub to answer the following questions.
Hunter
receives a pay stub from his job as an executive assistant. He is paid weekly. Due to a computer
glitch some of the calculations were replaced by “ *****”. Earnings
Statement Employee Name: Smith, Hunter Occupation: Writer/Editor Period End Date: March
20 Cheque Number: 1285 | Earnings | | | | | Deductions | | | Description | Hours | Rate | Amount | | Description | Amount | | Regular
Hours | 40 | 19.75 | ***** | | Income Tax | 203.99 | | Overtime | 2.5 | 29.63 | ***** | | EI | 14.92 | | Overtime | 0 | 39.50 | ***** | | CPP | 44.48 | | Vacation
Pay | | | 34.56 | | | | | Gross Pay | | | ***** | | Total Deductions | ***** | | | | | | | Net
Pay | ***** | | | | | | | |
|
|
|
40.
|
How much money did Hunter earn at a time and a half?
a. | $819.63 | b. | $148.15 | c. | $74.08 | d. | $859.13 |
|
Short Answer
|
|
|
1.
|
Quon is a chef. His regular pay is $21.35/h. If he works on a holiday, he
receives a shift premium of double time for those hours. Calculate his gross pay for the following
week. | Sunday | Monday - Holiday | Tuesday | Wednesday | Thursday | Friday | Saturday | | 8 h | 6 h | Day
Off | Day Off | 9 h | 5 h | 10 h | | | | | | | |
|
|
|
2.
|
Express 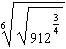 as a power with a rational exponent. Do not
evaluate.
|
|
|
3.
|
Using a graph, determine the number of solutions for the following linear
system. 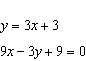 
|
|
|
4.
|
Is the point 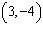 a solution to the system of equations? Justify your
answer. 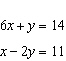
|
|
|
5.
|
Company A charges an initial setup fee of $105 and $25 a month for internet.
Company B charges an initial setup fee of $75 and $30 a month for internet. After how many months
would the two options cost the same?
|
Problem
|
|
|
1.
|
What is the edge length of a cube that has the same volume as the rectangular
prism below? 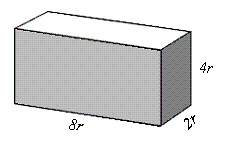
|
|
|
2.
|
The distance-time graph illustrates Abigail’s walk in front of a motion
sensor. 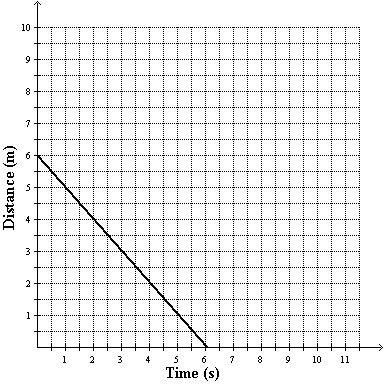 a) a) Identify the slope and explain what it
means. b) How long did it take Abigail to be 2.5 m from the sensor?
|
|
|
3.
|
The local hockey arena sells tickets for $200 each for platinum seats that are
closest to the ice. The arena charges $50 for gold seats that are farther back. The arena wants to
earn at least $200 000 from the platinum and gold seats at each game. The numbers of platinum tickets
sold for the first three games of the hockey season were 600, 550, and 500, respectively.
a) Write an equation in slope-intercept form that relates the number of gold and platinum
seats sold when $200 000 in revenue is generated.
b) How many gold seats must be sold for
each of the first three games to reach their revenue target for each game?
|
|
|
4.
|
The initial cost for Mason and his band to record their first CD was $1500. Each
CD will cost $5 to produce. If they sell their CDs for $10 each, how many must they sell before they
make a profit?
|