Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Evaluate 0.0013.
a. | 0.001 | b. | 0.000001 | c. | 0 | d. | 0.000000001 |
|
|
|
2.
|
Which description about the number 462 is correct?
a. | both a perfect cube and a perfect square | b. | perfect
square | c. | perfect cube | d. | neither a perfect cube nor a perfect
square |
|
|
|
3.
|
Evaluate 20 + 2–2.
a. | 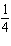 | b. | –4 | c. | 4 | d. | 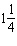 |
|
|
|
4.
|
Simplify 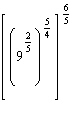 .
|
|
|
5.
|
Eric deposits $0.09 into a bank account that doubles the amount of money in the
account every year. After 1 year the value of the account is $0.18, and after 2 years it is $0.36.
What will the value of the account be after 15 years?
a. | $96 636 764.16 | b. | $2949.12 | c. | $2.70 | d. | $5898.24 |
|
|
|
6.
|
For what value of x do 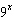 , 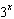 , and 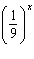 have the same
value? a. | x = 0 | b. | 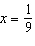 | c. | x =
9 | d. | x = 3 |
|
|
|
7.
|
Determine the product (x + 7)(x + 9).
a. | x2 + 7x + 63 | b. | x2 + 63x +
16 | c. | x2 + 16x + 63 | d. | x2 + 63x +
63 |
|
|
|
8.
|
Which pair of integers has a product of –60 and a sum of 4?
a. | –6 and 10 | b. | –6 and –10 | c. | 6 and
10 | d. | 6 and –10 |
|
|
|
9.
|
What is the factored form of 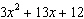 ?
|
|
|
10.
|
What is the factored form of 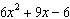 ?
|
|
|
11.
|
Determine the multiplication statement that is represented by the algebra tiles
below. 
|
|
|
12.
|
Which multiplication statement is represented by the algebra tiles
below? 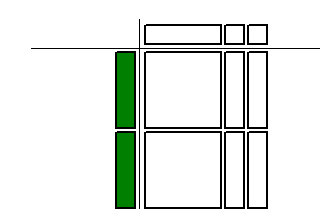
|
|
|
13.
|
Olivia walks to a friend’s house at a constant rate. After visiting for a
short time, Olivia and her friend start walking back to Olivia’s house. On the way, they meet
up with another friend. The three girls continue to walk at a slower pace. Olivia then realizes that
she is late and walks at a faster constant rate until she gets home. Which distance-time graph
represents this situation?
|
|
|
14.
|
How many of the four relations shown below are linear? 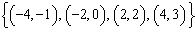
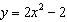 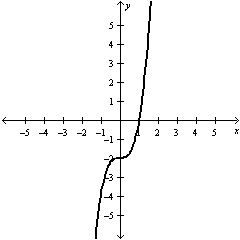 a. | Three of the above | b. | One of the above | c. | None of the
above | d. | Two of the above |
|
|
|
15.
|
Which scenario can be represented by a discrete relation?
a. | the shoe sizes of everyone in a grade 10 mathematics class | b. | the speed of a
sky-diver from the time he jumps out of a plane to when thediver lands on the
ground | c. | the distance travelled by a car travelling at a constant speed | d. | the mass of a dog
from a puppy to adult |
|
|
|
16.
|
Which of the following represents the range of the relation 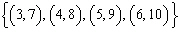 ?
|
|
|
17.
|
Which graph represents a relation that is not a function?
|
|
|
18.
|
Points 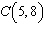 and 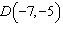 are on a line. What is the run from point
D to point C?
|
|
|
19.
|
The y-intercept of the line 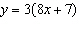 is
|
|
|
20.
|
Identify the equation of the line with a slope of –2 and a
y-intercept of –9.
|
|
|
21.
|
What are the slope and y-intercept of this line? 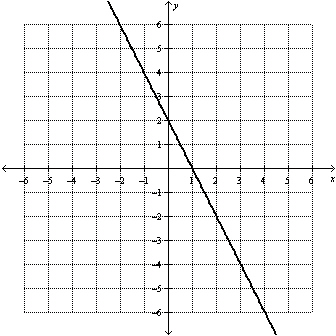 a. | slope: –2, y-intercept: 2 | b. | slope: –2, y-intercept:
–2 | c. | slope: 2, y-intercept: –2 | d. | slope: 2, y-intercept:
2 |
|
|
|
22.
|
When a linear equation is written in the form Ax + By + C =
0, A and B cannot both be __________.
a. | fractions | b. | one | c. | zero | d. | integers |
|
|
|
23.
|
Using the table of values, determine the y-intercept of the
line.
|
|
|
24.
|
Using the table of values, determine the slope of the line.
|
|
|
Answer the following questions using the information from the scenario
below.
Globo-Gym charges a flat fee of $20 per month plus $4.00 per visit. Average
Joe’s charges a flat fee of $30 per month plus $2.00 per visit. Let x represent the
number of visits per month and let y represent the total cost per month, in dollars.
|
|
|
25.
|
Identify the graph that represents this situation.
|
|
|
26.
|
Which of the following linear systems shows equivalent equations?
|
|
|
27.
|
Benjamin and Mia run a buffet-style restaurant. It costs them $2400.00 for rent
and utilities each month, plus an average of $5.00 per person for food. If they charge their
customers $12.50 each, what are the costs at the point where the costs equal the revenue?
a. | $4000.00 | b. | $2400.00 | c. | $2720.00 | d. | $2417.50 |
|
|
|
28.
|
Determine the solution to the linear system 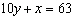 and 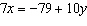 , using the
substitution method.
|
|
|
29.
|
Use the substitution method. The solution to the linear system 20x +
3y = –134 and –4x + 3y = 34 is
a. | (–7, 2) | b. | (7, 2) | c. | (7,
–2) | d. | (–7, –2) |
|
|
|
30.
|
In the triangle, RS = 8 cm and tan 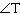 = 0.444. What is the length of
TS? 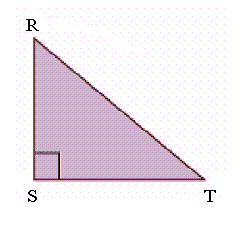 a. | 3.6 cm | b. | 18.0 cm | c. | 8.0
cm | d. | 19.7 cm |
|
|
|
31.
|
In 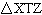 , 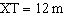 , 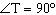 , and 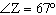 . Determine the
length of TZ, to the nearest metre.
|
|
|
32.
|
What is the cosine ratio of 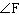 ? ?
|
|
|
33.
|
What is the value of sin 0°?
|
|
|
34.
|
What is the value of cos 90°?
|
|
|
35.
|
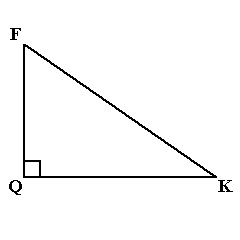
Determine the measure of 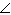 M, to the nearest degree. 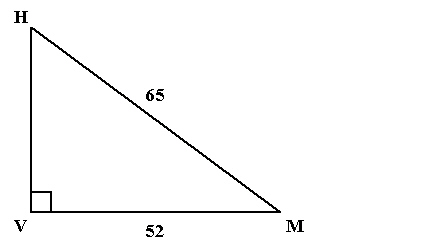
|
|
|
36.
|
The Canada Pension Plan (CPP) employee contribution rate is 4.95% of a
person’s gross pay up to a maximum of $2593.80 per year. The employer’s contribution rate
is 4.95% of a person’s gross pay up to a maximum of $2593.80 per year. How much did the
government collect in CPP payments for the year if the employee made $74 000.00 for the year?
a. | $2593.80 | b. | $3890.70 | c. | $5187.60 | d. | $3663.00 |
|
|
|
37.
|
Mei works at a candy store on Monday night where she earns $249.85 per month.
Mei uses this money to pay for her cell phone plan that is $42/month, a transit pass for $49/month,
and a yoga class for $50/month. If Mei wants to save $250 for a new bike, and she saves 40% of her
paycheque per month, how long will it take to save the money?
a. | 4 months | b. | 5 months | c. | 7
months | d. | 6 months |
|
|
|
38.
|
Jamal is hired by the Ministry of Forests to plant trees for the summer. On
average he plants 3300 trees per week and is paid $0.16 per tree. What is Jamal’s net pay at
the end of the 2 weeks, if he has deductions of $121.44, $26.14 and $8.76 taken from his paycheque
each week for income tax, CPP, and EI respectively?
a. | $743.32 | b. | $371.66 | c. | $528.00 | d. | $1056.00 |
|
|
|
39.
|
Mirka receives a pay stub from she job as an athletic trainer. She is paid
weekly. Earnings Statement Employee Name: Smith, Mirka Occupation: Executive
Assistant Period End Date: March 20 Cheque Number: 1274 | Earnings | | | | | Deductions | | | Description | Hours | Rate | Amount | | Description | Amount | | Regular Hours | 40 | 15.25 | 610.00 | | Income Tax | 415.94 | | Overtime | 10 | 22.88 | 228.75 | | EI | 33.01 | | Overtime | 19 | 30.50 | 579.50 | | CPP | 99.76 | | Vacation
Pay | | | 56.73 | | | | | Gross Pay | | | 1474.98 | | Total Deductions | 548.71 | | | | | | | Net
Pay | ***** | | | | | | | |
Due to a
computer glitch her Net Pay was not shown. What was Mirka’s net pay for the pay
period? a. | $1966.96 | b. | $2023.69 | c. | $926.27 | d. | $1097.43 |
|
|
|
40.
|
Lucas receives a pay stub from his job as an executive assistant. He is paid
bi-weekly. Earnings Statement Employee Name: Wong, Lucas Occupation: Athletic
Trainer Period End Date: June 18 Cheque Number: 1317 | Earnings | | | | | Deductions | | | Description | Hours | Rate | Amount | | Description | Amount | | Regular
Hours | 80 | 20.50 | 1640.00 | | Income Tax | 748.02 | | Overtime | 18 | 30.75 | 553.50 | | EI | 21.46 | | Overtime | 0 | 41.00 | 0.00 | | CPP | 64.85 | | Vacation
Pay | | | 87.74 | | | | | Gross Pay | | | 2281.24 | | Total Deductions | 834.33 | | | | | | | Net
Pay | 1446.91 | | | | | | | |
What
is Lucas’s gross pay for the year? a. | $118 624.48 | b. | $54 749.76 | c. | $59
312.24 | d. | $27 374.88 |
|
Short Answer
|
|
|
1.
|
Evaluate 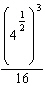 using a calculator. Express the answer to four decimal
places, where necessary.
|
|
|
2.
|
Factor the trinomial 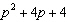 .
|
|
|
3.
|
|
|
|
4.
|
Write the equation in slope-intercept form for the line that passes through
points 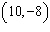 and 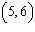 ?
|
|
|
5.
|
Is the point 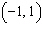 a solution to the system of equations? Support your answer
algebraically. 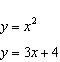
|
Problem
|
|
|
1.
|
A farmer uses a conveyor belt to move grain from ground level into a storage
silo. The conveyor has a length of 5 metres. Its angle of elevation can be adjusted from 5° to
20°. The silo has an opening that can accommodate the conveyor belt at its lowest and highest
settings. Determine the size of the opening of the silo, to the nearest tenth of a metre. 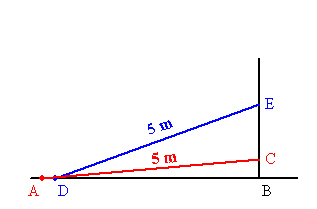
|
|
|
2.
|
An amount of $1000 is deposited in a savings account and earns simple interest.
The table shows the amount of money in the account at the end of each year.
Year | Amount
($) | 0 | 1000 | 1 | 1100 | 2 | 1200 | 3 | 1300 | | |
a) Is this a linear or
non-linear relation? Explain. b) Graph the relation.  c) c)
Which is the dependent variable? Which is the independent variable? d) How long
will it take for the account to reach a value of $1600?
|
|
|
3.
|
Isabella earns $8 per hour working at a fast-food restaurant. She takes the bus
to and from work for a total of $2 per day. Isabella’s daily net earnings can be represented by
the function 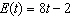 . a) Make a table of values of
Isabella’s net earnings for values of t from 0 to 4. b) Graph the
relation.  c) c) How much does Isabella earn if she works
for 7 h?
|
|
|
4.
|
Canada’s highest summits are located in the Yukon Territory. Two of these
include Mount Saint Elias and Mount Steele. The heights of these two mountains are related by the
following system of equations, where x and y represent the height of Mount Saint Elias
and Mount Steele in metres, respectively. 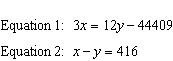
Use the
method of substitution to determine the two heights.
|