Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Identify two like terms and state how they are related.
–10x +
20y = 460
30x + 60y = 1620
a. | –10x and 30x; by a factor of –3 | c. | 30x and
60y; by a factor of 2 | b. | –10x and 20y; by a
factor of –2 | d. | –10x and 460; by a factor of 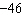 |
|
|
|
2.
|
Identify two like terms and state how they are related. 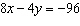 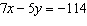 a. | 7x and –5y; by a factor of 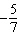 | c. | 8x and
–4y; by a factor of 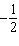 | b. | 8x and
–96; by a factor of 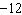 | d. | 8x and 7x; by a factor of 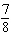 |
|
|
|
3.
|
For each equation, identify a number you could multiply each term by to ensure
that the coefficients of the variables and the constant term are
integers. (1) 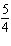 x x + 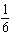 y y = 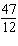 (2)
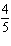 x x – 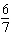 y y = 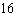 a. | Multiply equation (1) by 35; multiply equation (2) by 12. | b. | Multiply equation
(1) by 12; multiply equation (2) by 35. | c. | Multiply equation (1) by 2; multiply equation
(2) by 3. | d. | Multiply equation (1) by 3; multiply equation (2) by
2. |
|
|
|
4.
|
|
|
|
5.
|
The first equation of a linear system is 2x + 3y = 52. Choose a
second equation to form a linear system with infinite solutions.
i) 2x + 3y
= –260 ii) –10x – 15y =
–260 iii) –10x + 3y =
–260 iv) –10x + 3y = 255
a. | Equation iii | b. | Equation iv | c. | Equation i | d. | Equation
ii |
|
|
|
6.
|
Use substitution to solve this problem:
Tanukah invested a total of $4350 in
two bonds. He invested in one bond at an annual interest rate of 6% and in another bond at an annual
interest rate of 8%. After one year, the total interest earned was $324.00. How much money did
Tanukah invest in each bond?
a. | $3150 at 6%,
$1200 at 8% | b. | $1200 at 6%,
$3150 at 8%
| c. | $3650 at 6%,
$700 at 8% | d. | $700 at 6%,
$3650 at 8%
|
|
|
|
7.
|
The solution of this linear system is (–3, y). Determine the value
of y. x – 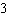 y = y = 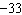
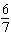 x – y
= x – y
= 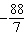
|
|
|
8.
|
The solution of this linear system is (–28, y). Determine the value
of y.
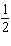 x – x – 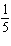 y = y = 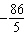
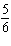 x – x – 4 y = 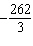
|
|
|
9.
|
Use an elimination strategy to solve this linear system. 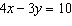 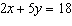
|
|
|
10.
|
Use an elimination strategy to solve this linear system. 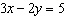 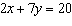
|
|
|
11.
|
Use an elimination strategy to solve this linear system. 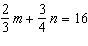 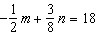
|
|
|
12.
|
Model this situation with a linear system:
At a campground, 5 large tanks and
5 small tanks contained 3200 L of drinking water. When one of the small tanks was replaced with a
large tank, there was 3400 L of drinking water.
|
|
|
13.
|
Use an elimination strategy to solve this linear system. 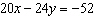 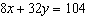
|
|
|
14.
|
Use an elimination strategy to solve this linear system. 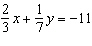 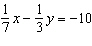
|
|
|
15.
|
Which linear system is modelled by these balance scales? (Each small square on
the right side of the balance scales represents 2 kg.) 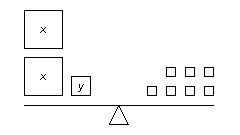 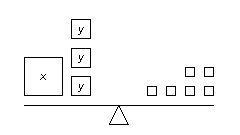
|
|
|
16.
|
Which linear system is modelled by these balance scales? (Each small square on
the right side of the balance scales represents 2 kg.) 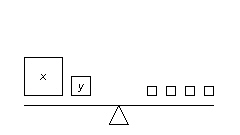 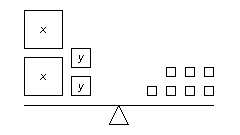
|
|
|
17.
|
Without graphing, determine the slope of the graph of the equation:
3x +
4y = 11
a. | 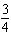 | b. | –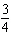 | c. | 4 | d. | 3 |
|
|
|
18.
|
Without graphing, determine which of these equations represent parallel
lines.
i) –6x + 6y = 12
ii) –4x + 6y =
12
iii) –2x + 6y = 12
iv) –6x + 6y =
14
a. | ii and iii | b. | i and ii | c. | i and iv | d. | i and
iii |
|
|
|
19.
|
Determine the number of solutions of the linear system:
14x +
7y = 315
16x – 2y = 610
a. | no solution | c. | two solutions | b. | one solution | d. | infinite
solutions |
|
|
|
20.
|
For what value of k does the linear system below have infinite
solutions? 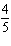 x + y = x + y = 14 kx + 2 y = 28 a. | 28 | b. | 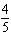 | c. | 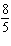 | d. | 0 |
|
Short Answer
|
|
|
21.
|
Identify two like terms and say how they are related.
6x + 4y =
–258
–3x + 5y = 45
|
|
|
22.
|
Create a linear system to model this situation. Then use substitution to solve
the linear system to solve the problem.
Bobbie has been saving dimes and quarters to buy a new
toy. She has a total of 28 dimes and quarters, with a value of $4.30. How many of each type of coin
does Bobbie have?
|
|
|
23.
|
Model this situation with a linear system:
The perimeter of a rectangle is
234 ft. When its length is doubled, the perimeter increases by 58 ft.
|
|
|
24.
|
Determine the number of solutions of this linear system.
7x –
3y = 43
7x – 3y = 13
|
|
|
25.
|
For what values of k does the linear system below
have: a) infinite
solutions? b) one solution? c)
no solution? 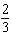 x x + y
= 16 kx + 3 y = 48
|
Problem
|
|
|
26.
|
Use a substitution strategy to solve the following problem.
Vivian
invested a total of $5600 in two bonds. She invested in one bond at 2% per annum and in another bond
at 5% per annum. In one year, the interest earned on each bond was the same. How much did Vivian
invest in each bond?
|
|
|
27.
|
Use an elimination strategy to solve this linear
system. Verify the solution.
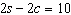 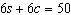
|
|
|
28.
|
Use the equation 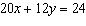 as an equation in three different linear systems. Write a
second equation so that each system has a different number of solutions. Explain what you did for
each system.
|
|
|
29.
|
Explain what happens when you try to solve this linear system using an
elimination strategy. What does this tell you about the graphs of these equations? 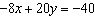 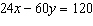
|
|
|
30.
|
Determine the number of solutions of this linear system. 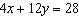 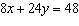
|