Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Identify two like terms and state how they are related.
–10x +
20y = 460
30x + 60y = 1620
a. | –10x and 30x; by a factor of –3 | c. | 30x and
60y; by a factor of 2 | b. | –10x and 20y; by a
factor of –2 | d. | –10x and 460; by a factor of 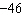 |
|
|
|
2.
|
For each equation, identify a number you could multiply each term by to ensure
that the coefficients of the variables and the constant term are
integers. (1) 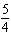 x x + 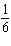 y y = 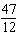 (2)
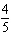 x x – 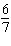 y y = 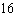 a. | Multiply equation (1) by 35; multiply equation (2) by 12. | b. | Multiply equation
(1) by 12; multiply equation (2) by 35. | c. | Multiply equation (1) by 2; multiply equation
(2) by 3. | d. | Multiply equation (1) by 3; multiply equation (2) by
2. |
|
|
|
3.
|
|
|
|
4.
|
Write an equivalent linear system where both equations have the same
y-coefficients. 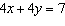 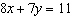
|
|
|
5.
|
The first equation of a linear system is –6x + 12y =
–42. Choose a second equation to form a linear system with no solution.
i)
–6x + 12y = 126 ii) 18x –
36y = 126 iii) 18x + 12y =
126 iv) 18x + 36y = 0
a. | Equation iv | b. | Equation ii | c. | Equation iii | d. | Equation
i |
|
|
|
6.
|
Use substitution to solve this linear system.
x = 2y –
56
5x + 13y = 410
a. | (4, –30) | b. | (–4, 30) | c. | (4, 30) | d. | (–4,
–30) |
|
|
|
7.
|
Use substitution to solve this linear system: x – y =
18 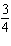 x x + 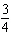 y y = 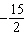 a. | x = 4; y = 18 | b. | x = –14; y =
–14 | c. | x = 4; y = –14 | d. | x = 4; y =
4 |
|
|
|
8.
|
The solution of this linear system is (–28, y). Determine the value
of y.
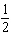 x – x – 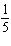 y = y = 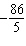
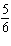 x – x – 4 y = 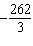
|
|
|
9.
|
Use an elimination strategy to solve this linear system. 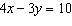 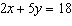
|
|
|
10.
|
Use an elimination strategy to solve this linear system. 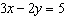 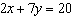
|
|
|
11.
|
Use an elimination strategy to solve this linear system. 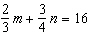 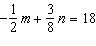
|
|
|
12.
|
Model this situation with a linear system:
Frieda has a 13% silver alloy and
a 31% silver alloy. Frieda wants to make 26 kg of an alloy that is 47% silver.
|
|
|
13.
|
Model this situation with a linear system:
At a campground, 5 large tanks and
5 small tanks contained 3200 L of drinking water. When one of the small tanks was replaced with a
large tank, there was 3400 L of drinking water.
|
|
|
14.
|
Model this situation with a linear system:
Nate borrowed $10 000 for his
university tuition. He borrowed part of the money at an annual interest rate of 2.4% and the rest of
the money at an annual interest rate of 4.5%. His total annual interest payment is $250.50.
|
|
|
15.
|
Without graphing, determine the slope of the graph of the equation:
3x +
4y = 11
a. | 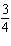 | b. | –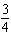 | c. | 4 | d. | 3 |
|
|
|
16.
|
Without graphing, determine which of these equations represent parallel
lines.
i) –6x + 6y = 12
ii) –4x + 6y =
12
iii) –2x + 6y = 12
iv) –6x + 6y =
14
a. | ii and iii | b. | i and ii | c. | i and iv | d. | i and
iii |
|
|
|
17.
|
Without graphing, determine the equation whose graph intersects the graph of
–6x + 3y = 11
exactly once.
i) –6x + 3y =
13
ii) –24x + 12y = 44
iii) –4x + 3y =
11
|
|
|
18.
|
Determine the number of solutions of the linear system:
14x +
7y = 315
16x – 2y = 610
a. | no solution | c. | two solutions | b. | one solution | d. | infinite
solutions |
|
|
|
19.
|
Determine the number of solutions of the linear system:
5x + 7y
= 76
–25x – 35y = –380
a. | 2 solutions | c. | infinite solutions | b. | one solution | d. | no solution |
|
|
|
20.
|
Two lines in a linear system have the same slope, but different
y-intercepts.
How many solutions does the linear system have?
a. | two solutions | c. | infinite solutions | b. | no solution | d. | one solution |
|
Short Answer
|
|
|
21.
|
Fill in the each blank below with the correct integer. System A
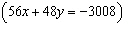 -____: -____:
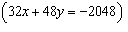 -____: -____: | System B
7x + 6y = –376
–4x –
6y = 256 | | |
|
|
|
22.
|
Identify two like terms and say how they are related.
6x + 4y =
–258
–3x + 5y = 45
|
|
|
23.
|
Determine the number of solutions of this linear system.
7x –
3y = 43
7x – 3y = 13
|
|
|
24.
|
Determine the number of solutions of this linear system.
15x +
30y = –240
17x + 21y = 53
|
|
|
25.
|
For what values of k does the linear system below
have: a) infinite
solutions? b) one solution? c)
no solution? 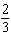 x x + y
= 16 kx + 3 y = 48
|
Problem
|
|
|
26.
|
Use a substitution strategy to solve the following problem.
Vivian
invested a total of $5600 in two bonds. She invested in one bond at 2% per annum and in another bond
at 5% per annum. In one year, the interest earned on each bond was the same. How much did Vivian
invest in each bond?
|
|
|
27.
|
Use a substitution strategy to solve the following problem.
Two isosceles
triangles have the same base length. The equal sides of one of the triangles
are 3.25 times as
long as the equal sides of the other. Find the lengths of the sides of the triangles when their
perimeters are 38 cm and 96.5 cm.
|
|
|
28.
|
Use an elimination strategy to solve this linear
system. Verify the solution.
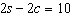 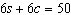
|
|
|
29.
|
Explain what happens when you try to solve this linear system using a
substitution strategy. What does this indicate about the graphs of these equations? 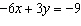 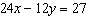
|
|
|
30.
|
Determine the number of solutions of this linear system. 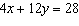 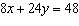
|