Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
For each equation, identify a number you could multiply each term by to ensure
that the coefficients of the variables and the constant term are
integers. (1) 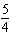 x x + 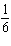 y y = 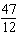 (2)
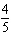 x x – 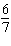 y y = 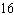 a. | Multiply equation (1) by 35; multiply equation (2) by 12. | b. | Multiply equation
(1) by 12; multiply equation (2) by 35. | c. | Multiply equation (1) by 2; multiply equation
(2) by 3. | d. | Multiply equation (1) by 3; multiply equation (2) by
2. |
|
|
|
2.
|
|
|
|
3.
|
For each equation, choose a divisor that is an integer. Then create an
equivalent linear system by dividing each term of the equation by the divisor.
12x –
8y = 1480
20x + 65y =
1370
a. | x – 3y = 370
x +
13y = 274 | c. | 3x – 2y = 370
4x +
13y = 274 | b. | 2x – 3y =
370
4x + 13y = 274 | d. | 3x – y =
370
4x + y = 274 |
|
|
|
4.
|
The first equation of a linear system is 8x + 13y = 166. Choose a
second equation to form a linear system with exactly one solution.
i) 8x +
13y = –830 ii) –40x – 65y
= –830 iii) –40x + 13y =
–830 iv) –40x – 65y =
0
a. | Equation iii | b. | Equation i | c. | Equation ii | d. | Equation
iv |
|
|
|
5.
|
The first equation of a linear system is –6x + 12y =
–42. Choose a second equation to form a linear system with no solution.
i)
–6x + 12y = 126 ii) 18x –
36y = 126 iii) 18x + 12y =
126 iv) 18x + 36y = 0
a. | Equation iv | b. | Equation ii | c. | Equation iii | d. | Equation
i |
|
|
|
6.
|
Use substitution to solve this linear system. y = 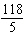 –
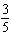 x x13 x + 5 y = 178 a. | (6, –20) | b. | (6, 20) | c. | (–6,
–20) | d. | (–6, 20) |
|
|
|
7.
|
Use substitution to solve this problem:
Tanukah invested a total of $4350 in
two bonds. He invested in one bond at an annual interest rate of 6% and in another bond at an annual
interest rate of 8%. After one year, the total interest earned was $324.00. How much money did
Tanukah invest in each bond?
a. | $3150 at 6%,
$1200 at 8% | b. | $1200 at 6%,
$3150 at 8%
| c. | $3650 at 6%,
$700 at 8% | d. | $700 at 6%,
$3650 at 8%
|
|
|
|
8.
|
Use substitution to solve this problem:
Wai Sen scored 85% on part A of a
math test and 95% on part B of the math test. Her total mark for the test was 70. The total mark
possible for the test was 78.
How many marks is each part worth?
a. | Part A: 37 marks; part B: 37 marks | c. | Part A: 37 marks; part B: 41
marks | b. | Part A: 41 marks; part B: 41 marks | d. | Part A: 41 marks; part B: 37
marks |
|
|
|
9.
|
Use substitution to solve this linear system: x – y =
18 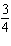 x x + 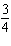 y y = 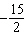 a. | x = 4; y = 18 | b. | x = –14; y =
–14 | c. | x = 4; y = –14 | d. | x = 4; y =
4 |
|
|
|
10.
|
The solution of this linear system is (–3, y). Determine the value
of y. x – 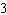 y = y = 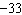
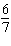 x – y
= x – y
= 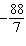
|
|
|
11.
|
Use an elimination strategy to solve this linear system. 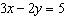 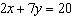
|
|
|
12.
|
Use an elimination strategy to solve this linear system. 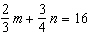 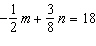
|
|
|
13.
|
Model this situation with a linear system:
Frieda has a 13% silver alloy and
a 31% silver alloy. Frieda wants to make 26 kg of an alloy that is 47% silver.
|
|
|
14.
|
Use an elimination strategy to solve this linear system. 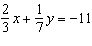 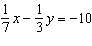
|
|
|
15.
|
Which linear system is modelled by these balance scales? (Each small square on
the right side of the balance scales represents 2 kg.) 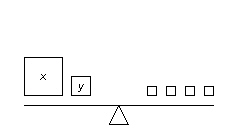 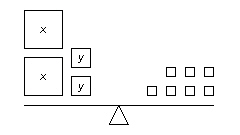
|
|
|
16.
|
Model this situation with a linear system:
Nate borrowed $10 000 for his
university tuition. He borrowed part of the money at an annual interest rate of 2.4% and the rest of
the money at an annual interest rate of 4.5%. His total annual interest payment is $250.50.
|
|
|
17.
|
Without graphing, determine which of these equations represent parallel
lines.
i) –6x + 6y = 12
ii) –4x + 6y =
12
iii) –2x + 6y = 12
iv) –6x + 6y =
14
a. | ii and iii | b. | i and ii | c. | i and iv | d. | i and
iii |
|
|
|
18.
|
Determine the number of solutions of the linear system:
14x +
7y = 315
16x – 2y = 610
a. | no solution | c. | two solutions | b. | one solution | d. | infinite
solutions |
|
|
|
19.
|
Determine the number of solutions of the linear system:
5x + 7y
= 76
–25x – 35y = –380
a. | 2 solutions | c. | infinite solutions | b. | one solution | d. | no solution |
|
|
|
20.
|
Two lines in a linear system have the same slope, but different
y-intercepts.
How many solutions does the linear system have?
a. | two solutions | c. | infinite solutions | b. | no solution | d. | one solution |
|
Short Answer
|
|
|
21.
|
Identify two like terms and say how they are related.
6x + 4y =
–258
–3x + 5y = 45
|
|
|
22.
|
Use an elimination strategy to solve this linear system. 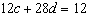 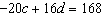
|
|
|
23.
|
Use an elimination strategy to solve this linear system. 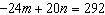 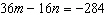
|
|
|
24.
|
Model this situation with a linear system:
A recycling depot pays 0.06¢
for a small can and 0.23¢ for a large can. Chara took 70 cans to the recycling depot and her
total refund was $22.35.
|
|
|
25.
|
Determine the number of solutions for the linear system that models this
problem:
Erica paid $6.00 for a bottle of water and 3 granola bars. Her friend paid $12.00 for
2 bottles of water and 6 granola bars. How much does a bottle of water cost?
|
Problem
|
|
|
26.
|
a) Write a linear system to model the
situation: A sports club charges an initiation fee and a monthly
fee. At the end of 5 months, a member had paid a total of $450. At the end of 10 months, she had paid
a total of $500.
b) Solve the linear
system by substitution to solve the related problem: What are the
initiation fee and the monthly fee?
|
|
|
27.
|
Use a substitution strategy to solve the following problem.
Vivian
invested a total of $5600 in two bonds. She invested in one bond at 2% per annum and in another bond
at 5% per annum. In one year, the interest earned on each bond was the same. How much did Vivian
invest in each bond?
|
|
|
28.
|
a) Model this
situation with a linear system:
To rent a car, a person is
charged a daily rate and a fee for each kilometre driven. When Chena rented a car for 15 days and
drove 800 km, the charge was $715.00. When she rented the same car for 25 days and drove 2250 km, the
charge was $1512.50.
b)
Determine the daily rate and the fee for each kilometre driven. Verify the solution.
|
|
|
29.
|
Cashew nuts sell for $21.00/kg. Brazil nuts sell for $15.00/kg. A distributor
sold a total of 120 kg of cashew nuts and Brazil nuts for $2244. What mass of each type of nut was
sold?
|
|
|
30.
|
Use the equation 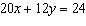 as an equation in three different linear systems. Write a
second equation so that each system has a different number of solutions. Explain what you did for
each system.
|