Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Which linear system has the solution x = –2 and y =
6?
a. | x + 3y = 16
4x + 4y = 16 | c. | x +
2y = –2
2x + 4y = –4 | b. | x + 3y
= 17
2x + y = 15 | d. | 2x + y = –2
x + y =
16 |
|
|
|
2.
|
Which linear system has the solution x = 4 and y =
–2?
a. | x + 4y = 15
4x 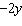 = –17 = –17 | c. | 4x +
y = 14
–2x 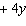 = –16 = –16 | b. | 2x + 4y = 4
–2x
+ y = 14 | d. | x +
4y = 4
2x + 4y = 8 |
|
|
|
3.
|
Which graph represents the solution of the linear system: y =
–2 x 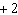 y + y + 6 = 2 x
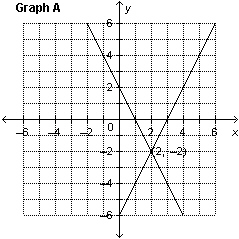 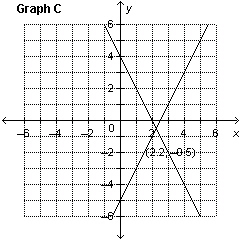 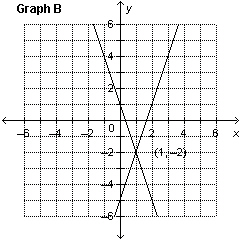 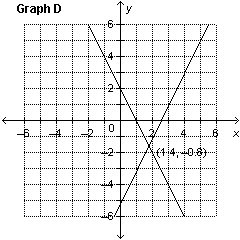 a. | Graph B | c. | Graph C | b. | Graph A | d. | Graph D |
|
|
|
4.
|
Which graph represents the solution of the linear system: –3 x
– y = –5 4 x – y =  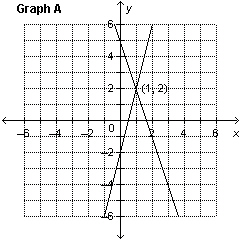 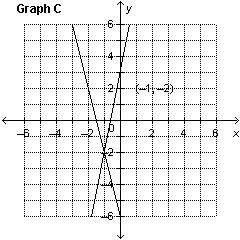 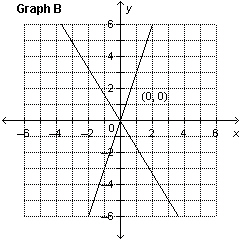 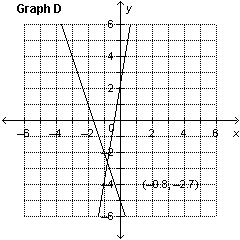 a. | Graph A | c. | Graph C | b. | Graph B | d. | Graph D |
|
|
|
5.
|
Use the graph to approximate the solution of this linear system: 6 x
– 7 y = –4
– 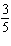 y y = 3 x + 7 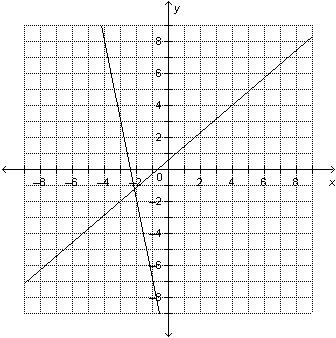 a. | (–0.1, 3.8) | b. | (–2.1, –1.2) | c. | (–1.2, 3.8) | d. | (–2.1,
–0.1) |
|
|
|
6.
|
Match each situation to a linear system below. A. The perimeter of a rectangular
playground is 163 m. The length is 6 m less than double
the
width.
B. The perimeter of a rectangular playground is
163 m. The width is one-half the length
decreased by 6 m. C.
The perimeter of a rectangular playground is 163 m. The length
decreased by 6 m is double the
width.
i) 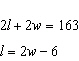 ii)
ii) 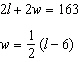 iii)
iii) 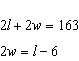 a. | A-i, B-ii, C-iii | c. | A-ii, B-i, C-iii | b. | A-iii, B-i, C-ii | d. | A-i, B-iii,
C-ii |
|
|
|
7.
|
Write a linear system to model this situation. Then verify which of the given
solutions is correct. A crate of 32 grapefruit has a total mass of 4.648 kg. When 9 grapefruit
are removed, the total mass is 3.622 kg. Verify the mass of the crate and the average mass of one
grapefruit. A. 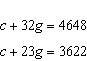 B. B. 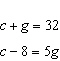 C. C. 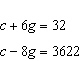 D. D. 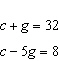 i) i)
The crate has a mass of 1 kg, and the mass of one grapefruit is
114 g. ii) The crate has a mass of 1.2 kg, and the
mass of one grapefruit is 114.2 g. iii) The crate has a mass
of 1 kg, and the mass of one grapefruit is 114.2 g. iv)
The crate has a mass of 1.2 kg, and the mass of one grapefruit is 57 g. a. | Part A-i | c. | Part B-iii | b. | Part C-ii | d. | Part D-iv |
|
|
|
8.
|
Use the graph to solve the linear system: y = –3 x –
5 y 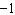 = 3 x  a. | (1, –2) | c. | (1, 0) | b. | (–1, 0) | d. | (–1,
–2) |
|
|
|
9.
|
Which linear system is represented by this graph? a) 2x –
5y = –16
x =
1
b) 2x + 5y = 16
2x – 5y =
16
c) 2x – 5y = 16
x – 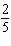 y = y =
–1
d) 2x + 5y = 16
x = –1
| 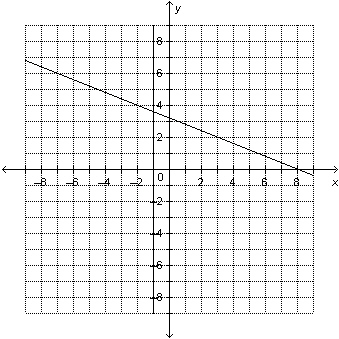 | | |
a. | System a | b. | System d | c. | System b | d. | System
c |
|
|
|
10.
|
Determine the solution of the linear system represented by this graph. a) (2, 3.8)
b) (3.8, 2)
c)
(–3, 3.8)
d) (–2, 3.8) | 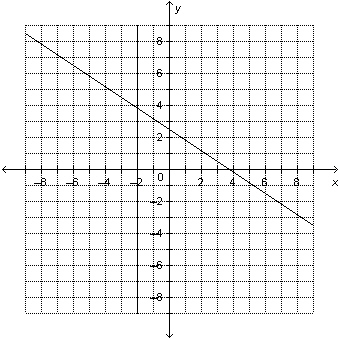 | | |
|
Short Answer
|
|
|
11.
|
Quincy used this linear system to represent a situation involving a collection
of $5 bills and $10 bills:
f + t = 70
5f + 10t = 575
a)
What problem might Quincy have written?
b)
What does each variable represent?
|
|
|
12.
|
Solve this linear system by graphing. y = –8
–3 x + y = 7 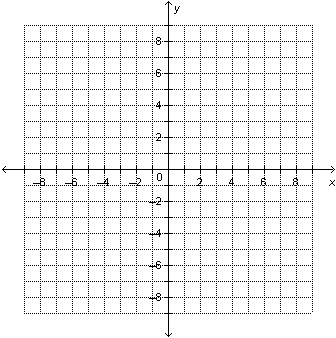
|
|
|
13.
|
a) Write a linear system to model this
situation: Angela is 24 years older than her cousin Zack. In 13
years, she will be double his age.
b) Use a graph to
solve this problem: How old are Angela and Zack now?
|
|
|
14.
|
Use graphing technology to solve this linear system.
Where necessary, write
the coordinates to the nearest tenth.
–3x – 5y = 12
–x
+ y = –10
|
Problem
|
|
|
15.
|
These balance scales illustrate the two different sizes of cartons of detergent:
x represents the mass of a large carton and y represents the mass of a small
carton. 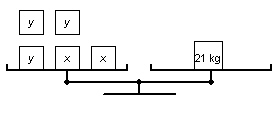 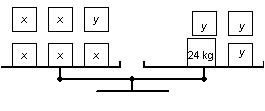 a) a)
Write a linear system to model the two balance scales. b) Use the diagrams of the balance
scales to verify that a large carton of detergent has a mass of 6 kg and a small carton has a mass of
3 kg.
c) Use the linear system to verify the masses of
the cartons in part b.
|
|
|
16.
|
a) Write a linear system whose solution
is: x = 5, y = –5.
b) Is there more than
one linear system with this solution? Explain.
|
|
|
17.
|
a) Use graphing technology to determine
the solution of this linear system. 17x + 10y =
9
7x – 6y = 29
b) Verify the
solution.
|