Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Which linear system has the solution x = 4 and y =
–2?
a. | x + 4y = 15
4x 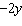 = –17 = –17 | c. | 4x +
y = 14
–2x 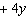 = –16 = –16 | b. | 2x + 4y = 4
–2x
+ y = 14 | d. | x +
4y = 4
2x + 4y = 8 |
|
|
|
2.
|
Which graph represents the solution of the linear system: y =
–2 x 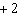 y + y + 6 = 2 x
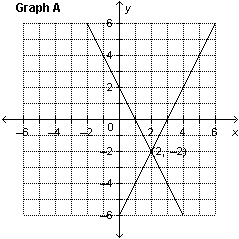 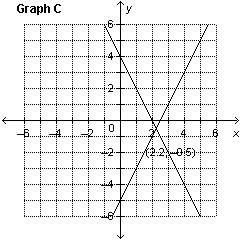 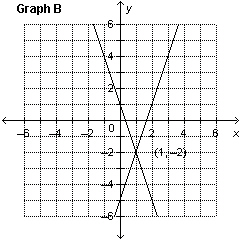 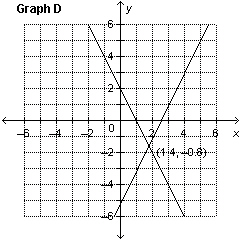 a. | Graph B | c. | Graph C | b. | Graph A | d. | Graph D |
|
|
|
3.
|
Two life insurance companies determine their premiums using different
formulas: Company A: p = 2 a + 24 Company B: p = 2.25 a + 13, where
p represents the annual premium, and a represents the client’s age. Use the
graph to determine the age at which both companies charge the same premium. 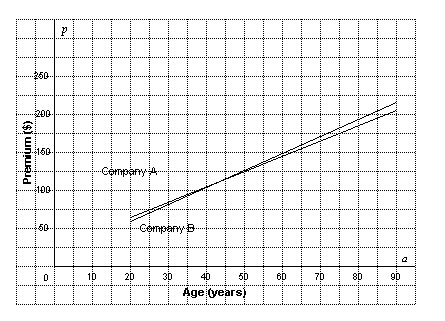 a. | 62 years | b. | 24 years | c. | 59 years | d. | 44 years
|
|
|
|
4.
|
Express each equation in slope-intercept form.
–2x + 4y =
68
13x + 4y = 284
|
|
|
5.
|
Use the table of values to determine the solution of this linear system:
a. | (–2, 2) | c. | (2, 2) | b. | (2,–2) | d. | (–2,
–2) |
|
|
|
6.
|
Create a linear system to model this situation:
In a board game, Judy scored
3 points more than twice the number of points Ann scored.
There was a total of 39 points
scored.
a. | j = 3 + 2a
j + a = 39 | b. | j – 3
= 2a
j + 2a = 39 | c. | j + 3 = 2a
j + a = 39 | d. | a = 3 + 2j
j + a =
39 |
|
|
|
7.
|
Create a linear system to model this situation:
Tickets for a school play
cost $8 for adults and $4.75 for students.
There were ten more student tickets sold than adult
tickets, and a total of $1399 in ticket sales was collected.
a. | 8a + 4.75s = 1399
s = a + 10 | c. | 8a +
4.75s = 1399
a = s + 10 | b. | 8a + 4.75s = 1399
a +
s = 10 | d. | 4.75a
+ 8s = 1399
s = a + 10 |
|
|
|
8.
|
Use the graph to solve the linear system: y = –5 x 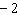 y + y + 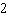 = 2 x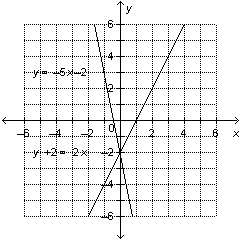 a. | (2, 0) | c. | (0, 0) | b. | (2, –2) | d. | (0, –2) |
|
|
|
9.
|
Which linear system is represented by this graph? a) x –
y = 5
5x + 6y =
18
b) x – y =
7
5x + 6y = 18
c)
x – y = 9
6x + 6y =
18
d) x – y = 11
6x + 5y = 18 | 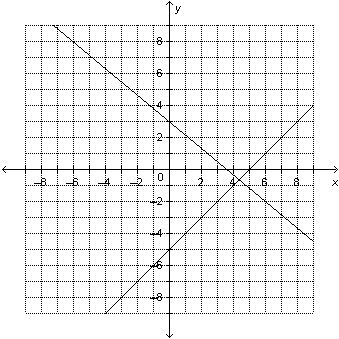 | | |
a. | System d | b. | System b | c. | System a | d. | System
c |
|
|
|
10.
|
Determine the solution of the linear system represented by this graph. a) (3, 5.3)
b) (5.3, 3)
c) (
5.3, –3)
d) (–4, 5.3)
| 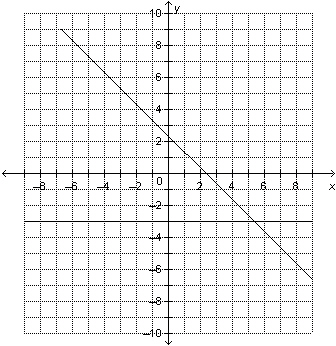 | | |
|
Short Answer
|
|
|
11.
|
Create a linear system to model this situation:
A sack of wheat costs $10.75
and a sack of oats costs $12.75. If the total cost was $778.75 and
65 sacks were ordered, how
many sacks of each grain were purchased?
Verify that 25 sacks of wheat and 40 sacks of oats
represent the solution of the linear system.
|
|
|
12.
|
Quincy used this linear system to represent a situation involving a collection
of $5 bills and $10 bills:
f + t = 70
5f + 10t = 575
a)
What problem might Quincy have written?
b)
What does each variable represent?
|
|
|
13.
|
Solve this linear system by graphing. –3 x – 2 y =
16 – x + y = –8 
|
|
|
14.
|
a) Write a linear system to model this
situation: Angela is 24 years older than her cousin Zack. In 13
years, she will be double his age.
b) Use a graph to
solve this problem: How old are Angela and Zack now?
|
Problem
|
|
|
15.
|
In a piggy bank, the number of nickels is 8 more than one-half the number of
quarters. The value of the coins is $21.85.
a) Create a
linear system to model the situation.
b) If the number of
quarters is 78, determine the number of nickels.
|
|
|
16.
|
These balance scales illustrate the two different sizes of cartons of detergent:
x represents the mass of a large carton and y represents the mass of a small
carton. 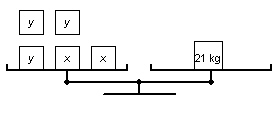 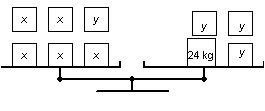 a) a)
Write a linear system to model the two balance scales. b) Use the diagrams of the balance
scales to verify that a large carton of detergent has a mass of 6 kg and a small carton has a mass of
3 kg.
c) Use the linear system to verify the masses of
the cartons in part b.
|
|
|
17.
|
a) Write a linear system to model this
situation. Mrs. Cheechoo paid $155 for one-day tickets to
Silverwood Theme Park for herself, her husband, and 3 children. Next month, she paid $285 for
herself, 3 adults, and 5 children.
b) Use a graph to
solve this problem: What are the prices of a one-day ticket for an
adult and for a child?
|