Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Which linear system has the solution x = –2 and y =
6?
a. | x + 3y = 16
4x + 4y = 16 | c. | x +
2y = –2
2x + 4y = –4 | b. | x + 3y
= 17
2x + y = 15 | d. | 2x + y = –2
x + y =
16 |
|
|
|
2.
|
Which graph represents the solution of the linear system: y =
–2 x 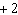 y + y + 6 = 2 x
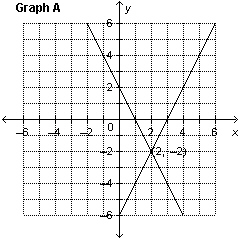 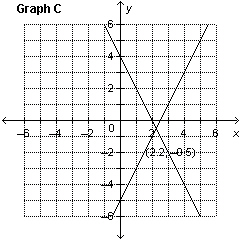  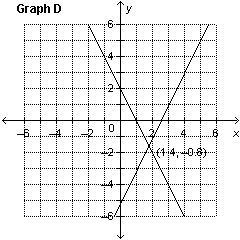 a. | Graph B | c. | Graph C | b. | Graph A | d. | Graph D |
|
|
|
3.
|
Which graph represents the solution of the linear system: –3 x
– y = –5 4 x – y = 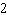 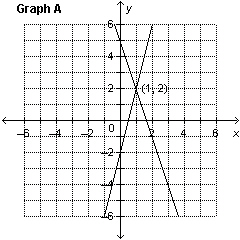 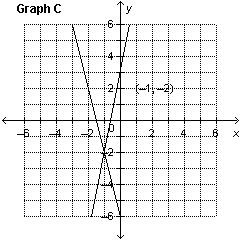 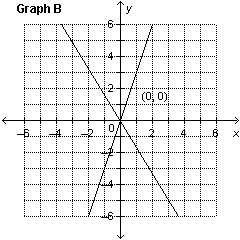 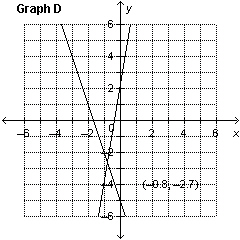 a. | Graph A | c. | Graph C | b. | Graph B | d. | Graph D |
|
|
|
4.
|
Car A left Calgary at 8 A.M. to travel 500 mi. to Regina, at an average speed of
63 mph. Car B left Regina at the same time to travel to Calgary at an average speed of 37
mph. A linear system that models this situation is: d = 500 – 63 t
d = 37 t,
where d is the distance in miles from Regina, and t is
the time in hours since 8 A.M. Which graph would you use to determine how far the cars are from
Regina when they meet? What is this distance? a. | Graph C:
195.8 mi. | b. | Graph D:
200 mi. | c. | Graph A:
185 mi. | d. | Graph B:
92.5
mi. |
|
|
|
5.
|
Use the graph to approximate the solution of this linear system: 6 x
– 7 y = –4
– 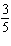 y y = 3 x + 7 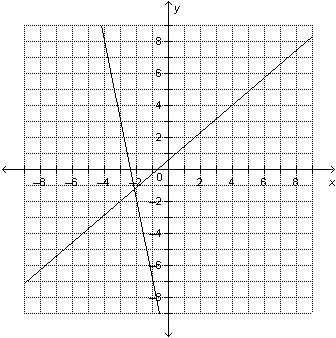 a. | (–0.1, 3.8) | b. | (–2.1, –1.2) | c. | (–1.2, 3.8) | d. | (–2.1,
–0.1) |
|
|
|
6.
|
Create a linear system to model this situation:
Cheri operates a
grass-cutting business. She charges $19 for a small lawn and $29 for a large lawn. One weekend, Cheri
made $287 by cutting 13 lawns.
a. | s + l = 13
19s + 29l = 287 | c. | s + l
= 13
29s + 19l = 287 | b. | s + l = 287
19s +
29l = 13 | d. | s + l = 287
29s + 19l =
13 |
|
|
|
7.
|
Yoshiko used this linear system to represent a situation involving the costs of
shirts and pants. 3 s + p = 144 4 s + 3 p = 122 What problem might
Yoshiko have solved? A. Three shirts and one pair of
pants cost $144. Four shirts and three pairs of pants cost $122. Determine the costs of one shirt and one pair
of pants.
B. Three shirts and one pair of pants cost
$144. Two shirts and three pairs of pants cost $122. Determine the costs of one shirt and one pair
of pants.
C. Three shirts cost $144. Four shirts and
three pairs of pants cost $122.
Determine the costs of one shirt and one pair of pants.
D.
Three shirts and 4 pairs of pants cost $144. Four shirts and three
pairs of pants cost $122. Determine
the costs of one shirt and one pair of pants.
a. | Problem D | b. | Problem A | c. | Problem C | d. | Problem
B |
|
|
|
8.
|
Use the graph to solve the linear system: y = –5 x 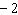 y + y + 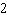 = 2 x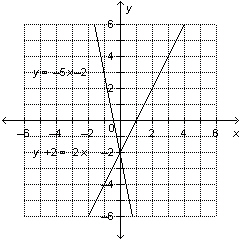 a. | (2, 0) | c. | (0, 0) | b. | (2, –2) | d. | (0, –2) |
|
|
|
9.
|
Which linear system is represented by this graph? a) x –
y = 5
5x + 6y =
18
b) x – y =
7
5x + 6y = 18
c)
x – y = 9
6x + 6y =
18
d) x – y = 11
6x + 5y = 18 | 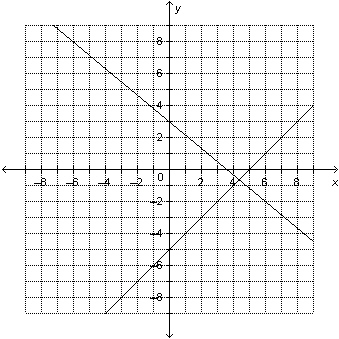 | | |
a. | System d | b. | System b | c. | System a | d. | System
c |
|
|
|
10.
|
Which linear system is represented by this graph? a) 2x –
5y = –16
x =
1
b) 2x + 5y = 16
2x – 5y =
16
c) 2x – 5y = 16
x – 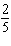 y = y =
–1
d) 2x + 5y = 16
x = –1
| 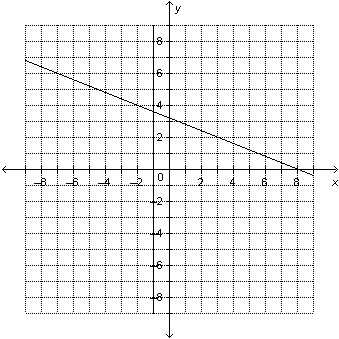 | | |
a. | System a | b. | System d | c. | System b | d. | System
c |
|
Short Answer
|
|
|
11.
|
Create a linear system to model this situation:
The cost of admission to the
museum is $5.50 for adults and $3.50 for students.
Yesterday, 100 admissions were sold, and the
receipts were $424.00.
|
|
|
12.
|
Solve this linear system by graphing. y = –8
–3 x + y = 7 
|
|
|
13.
|
a) Write a linear system to model this
situation: Angela is 24 years older than her cousin Zack. In 13
years, she will be double his age.
b) Use a graph to
solve this problem: How old are Angela and Zack now?
|
|
|
14.
|
a) Write a linear system to model this
situation: A hockey coach bought 25 pucks for a total cost of $70.
The pucks used for practice cost
$2.50 each, and the pucks
used for games cost $3.25 each.
b) Use a graph to
solve this problem: How many of each type of puck did the coach
purchase?
|
Problem
|
|
|
15.
|
These balance scales illustrate the two different sizes of cartons of detergent:
x represents the mass of a large carton and y represents the mass of a small
carton. 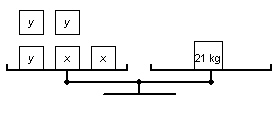 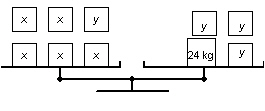 a) a)
Write a linear system to model the two balance scales. b) Use the diagrams of the balance
scales to verify that a large carton of detergent has a mass of 6 kg and a small carton has a mass of
3 kg.
c) Use the linear system to verify the masses of
the cartons in part b.
|
|
|
16.
|
a) Write a linear system to model this
situation. Mrs. Cheechoo paid $155 for one-day tickets to
Silverwood Theme Park for herself, her husband, and 3 children. Next month, she paid $285 for
herself, 3 adults, and 5 children.
b) Use a graph to
solve this problem: What are the prices of a one-day ticket for an
adult and for a child?
|
|
|
17.
|
Gino’s class was assigned the following two-part question for
homework.
a) Write a linear system to model this
situation: Save-Way-More food store received a delivery of 86 boxes
of apples and bananas. Each box of apples had a mass of 32 lb., and each box of bananas had a mass of
16 lb. The total mass of the delivery was 1968 lb.
b)
Use a graph to solve this problem: How many boxes of each fruit
were there?
Gino answered part a correctly, but could not understand why his solution of 49 boxes
of apples and 37 boxes of bananas was incorrect for part b. Explain what he likely did
wrong.
|