Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Use the table of values to determine the solution of this linear system:
a. | (–2, 2) | c. | (2, 2) | b. | (2,–2) | d. | (–2,
–2) |
|
|
|
2.
|
Use the table of values to determine the solution of this linear system:
a. | (–13, –13) | c. | (–13, 4) | b. | (4, –13) | d. | (4, 4) |
|
|
|
3.
|
Identify two like terms and state how they are related. 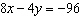 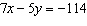 a. | 7x and –5y; by a factor of 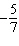 | c. | 8x and
–4y; by a factor of 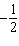 | b. | 8x and
–96; by a factor of 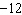 | d. | 8x and 7x; by a factor of 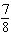 |
|
|
|
4.
|
Write an equivalent linear system where both equations have the same
y-coefficients. 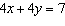 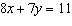
|
|
|
5.
|
The first equation of a linear system is 2x + 3y = 52. Choose a
second equation to form a linear system with infinite solutions.
i) 2x + 3y
= –260 ii) –10x – 15y =
–260 iii) –10x + 3y =
–260 iv) –10x + 3y = 255
a. | Equation iii | b. | Equation iv | c. | Equation i | d. | Equation
ii |
|
|
|
6.
|
Create a linear system to model this situation:
A collection of nickels and
dimes contains four times as many dimes as nickels. The total value of the collection is
$20.25.
a. | d = 4n
5n + 10d = 2025 | b. | d = 4n
5d +
10n = 2025 | c. | n = 4d
5n + 10d = 2025 | d. | d + n = 15
5n
+ 10d = 2025 |
|
|
|
7.
|
Create a linear system to model this situation:
A length of outdoor lights is
formed from strings that are 5 ft. long and 11 ft. long. Fourteen strings of lights are 106 ft.
long.
a. | 5x + 11y = 14
x + y = 106 | c. | x + y
= 14
5x + 11y = 106(14) | b. | x + y = 14
5x +
11y = 106 | d. | x +
y = 14
x + 2y = 106 |
|
|
|
8.
|
Yoshiko used this linear system to represent a situation involving the costs of
shirts and pants. 3 s + p = 144 4 s + 3 p = 122 What problem might
Yoshiko have solved? A. Three shirts and one pair of
pants cost $144. Four shirts and three pairs of pants cost $122. Determine the costs of one shirt and one pair
of pants.
B. Three shirts and one pair of pants cost
$144. Two shirts and three pairs of pants cost $122. Determine the costs of one shirt and one pair
of pants.
C. Three shirts cost $144. Four shirts and
three pairs of pants cost $122.
Determine the costs of one shirt and one pair of pants.
D.
Three shirts and 4 pairs of pants cost $144. Four shirts and three
pairs of pants cost $122. Determine
the costs of one shirt and one pair of pants.
a. | Problem D | b. | Problem A | c. | Problem C | d. | Problem
B |
|
|
|
9.
|
Write a linear system to model this situation. Then verify which of the given
solutions is correct. A crate of 32 grapefruit has a total mass of 4.648 kg. When 9 grapefruit
are removed, the total mass is 3.622 kg. Verify the mass of the crate and the average mass of one
grapefruit. A. 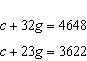 B. B. 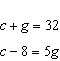 C. C. 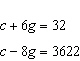 D. D. 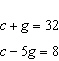 i) i)
The crate has a mass of 1 kg, and the mass of one grapefruit is
114 g. ii) The crate has a mass of 1.2 kg, and the
mass of one grapefruit is 114.2 g. iii) The crate has a mass
of 1 kg, and the mass of one grapefruit is 114.2 g. iv)
The crate has a mass of 1.2 kg, and the mass of one grapefruit is 57 g. a. | Part A-i | c. | Part B-iii | b. | Part C-ii | d. | Part D-iv |
|
|
|
10.
|
Use the graph to solve the linear system: y = –3 x –
5 y 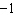 = 3 x 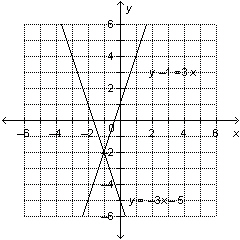 a. | (1, –2) | c. | (1, 0) | b. | (–1, 0) | d. | (–1,
–2) |
|
|
|
11.
|
Use the graph to solve the linear system: y = –5 x 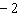 y + y + 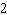 = 2 x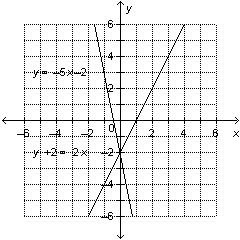 a. | (2, 0) | c. | (0, 0) | b. | (2, –2) | d. | (0, –2) |
|
|
|
12.
|
Determine the solution of the linear system represented by this graph. a) (3, 5.3)
b) (5.3, 3)
c) (
5.3, –3)
d) (–4, 5.3)
| 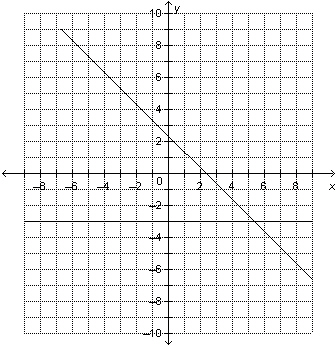 | | |
|
|
|
13.
|
Use substitution to solve this linear system. x = 4 + y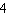 x
+ x
+ 16 y = –264 a. | (–14, –14) | b. | (–10, –10) | c. | (–10,
–14) | d. | (–14, –10) |
|
|
|
14.
|
Use substitution to solve this problem:
The perimeter of a rectangular field
is 276 m. The length is 18 m longer than the width.
What are the dimensions of the
field?
a. | 58 m by 80 m | b. | 68 m by 70 m | c. | 78 m by 60 m | d. | 48 m by 90 m
|
|
|
|
15.
|
Use an elimination strategy to solve this linear system. 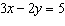 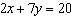
|
|
|
16.
|
Model this situation with a linear system:
At a campground, 5 large tanks and
5 small tanks contained 3200 L of drinking water. When one of the small tanks was replaced with a
large tank, there was 3400 L of drinking water.
|
|
|
17.
|
Model this situation with a linear system:
Nate borrowed $10 000 for his
university tuition. He borrowed part of the money at an annual interest rate of 2.4% and the rest of
the money at an annual interest rate of 4.5%. His total annual interest payment is $250.50.
|
|
|
18.
|
Without graphing, determine the equation whose graph intersects the graph of
–6x + 3y = 11
exactly once.
i) –6x + 3y =
13
ii) –24x + 12y = 44
iii) –4x + 3y =
11
|
|
|
19.
|
Determine the number of solutions of the linear system:
2x –
5y = 23
–6x + 15y = 21
a. | one solution | c. | two solutions | b. | no solution | d. | infinite
solutions |
|
|
|
20.
|
Determine the number of solutions for the linear system that models this
problem:
Two people are playing a game. The difference in their points is 83. When the number
of points each player has is doubled, the difference is 166. How many points does each person
have?
a. | one solution | c. | no solution | b. | two solutions | d. | infinite
solutions |
|
Short Answer
|
|
|
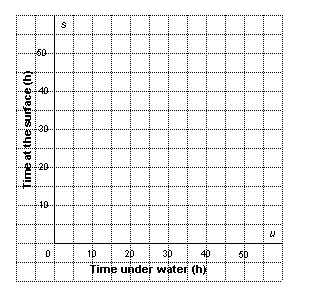
21.
|
A submarine cruises underwater at 20 km/h and on the surface at 30 km/h. The
submarine travels a distance of 650 km in 25 h. A linear system that models this situation
is: u + s = 25 20 u + 30 s = 650 where u represents the
time in hours cruising underwater, and s represents the time in hours cruising on the
surface. a) Graph the linear system above. b)
Use the graph to solve the problem: How long did the submarine travel underwater, and how long did it travel on
the surface?
|
|
|
22.
|
Fill in the each blank below with the correct integer. System A
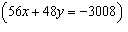 -____: -____:
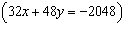 -____: -____: | System B
7x + 6y = –376
–4x –
6y = 256 | | |
|
|
|
23.
|
Use an elimination strategy to solve this linear system. 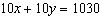 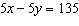
|
|
|
24.
|
Model this situation with a linear system:
The perimeter of a rectangle is
234 ft. When its length is doubled, the perimeter increases by 58 ft.
|
|
|
25.
|
Determine the number of solutions of this linear system.
7x –
3y = 43
7x – 3y = 13
|
Problem
|
|
|
26.
|
Sales clerks at an appliance store have a choice of two methods of
payment: Plan A: $580 every two weeks plus 4.2% commission on all sales Plan B: $880 every two
weeks plus 1.2% commission on all sales a) Write a linear
system to model this situation. b) Graph the linear system
in part a. c) Use the graph to solve this problem: What must the
sales for a two-week period be for a clerk to receive the same salary with both plans?
|
|
|
27.
|
Use a substitution strategy to solve the following problem.
Two isosceles
triangles have the same base length. The equal sides of one of the triangles
are 3.25 times as
long as the equal sides of the other. Find the lengths of the sides of the triangles when their
perimeters are 38 cm and 96.5 cm.
|
|
|
28.
|
a) Write a linear system to model the
situation: For the school play, the cost of one adult ticket is $6
and the cost of one student ticket is $4. Twice as many student tickets as adult tickets were sold.
The total receipts were $2016.
b) Use substitution to
solve the related problem: How many of each type of ticket were
sold?
|
|
|
29.
|
Use an elimination strategy to solve this linear
system. Verify the solution.
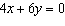 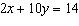
|
|
|
30.
|
Use an elimination strategy to solve this linear
system. Verify the solution.
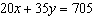 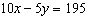
|