Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Which linear system has the solution x = –2 and y =
6?
a. | x + 3y = 16
4x + 4y = 16 | c. | x +
2y = –2
2x + 4y = –4 | b. | x + 3y
= 17
2x + y = 15 | d. | 2x + y = –2
x + y =
16 |
|
|
|
2.
|
At a skating rink, admission is $4.00 for a student and $8.00 for an adult.
Tuesday evening, 20 people used the skating rink and a total of $132 in admission fees was
collected. A linear system that models this situation is: 4 s + 8 a =
132 s +
a = 20
where s represents the number of student admissions, and
a represents the number of adult admissions purchased. Use the graph to solve this
problem: How many students used the skating rink on Tuesday evening? 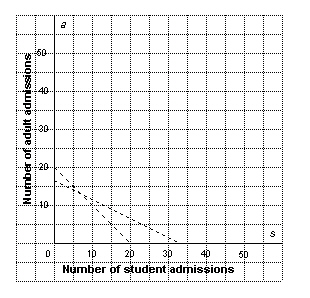 a. | 19 students | b. | 20 students | c. | 13 students | d. | 7
students |
|
|
|
3.
|
Use the table of values to determine the solution of this linear system:
a. | (–13, –13) | c. | (–13, 4) | b. | (4, –13) | d. | (4, 4) |
|
|
|
4.
|
Write an equivalent linear system where both equations have the same
y-coefficients. 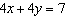 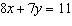
|
|
|
5.
|
The first equation of a linear system is 8x + 13y = 166. Choose a
second equation to form a linear system with exactly one solution.
i) 8x +
13y = –830 ii) –40x – 65y
= –830 iii) –40x + 13y =
–830 iv) –40x – 65y =
0
a. | Equation iii | b. | Equation i | c. | Equation ii | d. | Equation
iv |
|
|
|
6.
|
Create a linear system to model this situation:
A woman is 3 times as old as
her son. In thirteen years, she will be 2 times as old as her son will be.
a. | w = s + 3
w + 13 = 2s | c. | w = 3s
w =
2s | b. | w = 3s
w + 13 = 2(s + 13) | d. | w = 3s
s + 13 =
2(w + 13) |
|
|
|
7.
|
Create a linear system to model this situation:
A length of outdoor lights is
formed from strings that are 5 ft. long and 11 ft. long. Fourteen strings of lights are 106 ft.
long.
a. | 5x + 11y = 14
x + y = 106 | c. | x + y
= 14
5x + 11y = 106(14) | b. | x + y = 14
5x +
11y = 106 | d. | x +
y = 14
x + 2y = 106 |
|
|
|
8.
|
Create a linear system to model this situation:
A rectangular field is 35 m
longer than it is wide. The length of the fence around
the perimeter of the field is 290
m.
a. | l + 35 = w
2l + 2w = 290 | b. | l = w
+ 35
2l + 2w = 290 | c. | l = w + 35
l + w =
290 | d. | l = w + 35
lw = 290 |
|
|
|
9.
|
Yoshiko used this linear system to represent a situation involving the costs of
shirts and pants. 3 s + p = 144 4 s + 3 p = 122 What problem might
Yoshiko have solved? A. Three shirts and one pair of
pants cost $144. Four shirts and three pairs of pants cost $122. Determine the costs of one shirt and one pair
of pants.
B. Three shirts and one pair of pants cost
$144. Two shirts and three pairs of pants cost $122. Determine the costs of one shirt and one pair
of pants.
C. Three shirts cost $144. Four shirts and
three pairs of pants cost $122.
Determine the costs of one shirt and one pair of pants.
D.
Three shirts and 4 pairs of pants cost $144. Four shirts and three
pairs of pants cost $122. Determine
the costs of one shirt and one pair of pants.
a. | Problem D | b. | Problem A | c. | Problem C | d. | Problem
B |
|
|
|
10.
|
Use the graph to solve the linear system: y = –3 x –
5 y 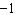 = 3 x 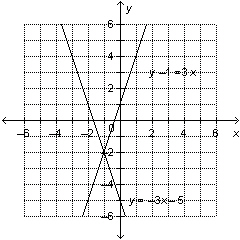 a. | (1, –2) | c. | (1, 0) | b. | (–1, 0) | d. | (–1,
–2) |
|
|
|
11.
|
Determine the solution of the linear system represented by this graph. a) (2, 3.8)
b) (3.8, 2)
c)
(–3, 3.8)
d) (–2, 3.8) | 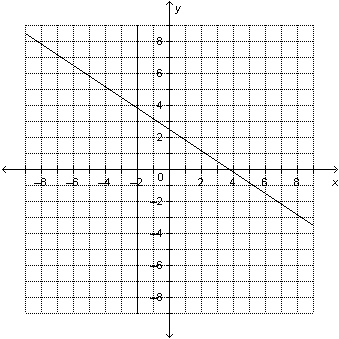 | | |
|
|
|
12.
|
Use substitution to solve this problem:
Tanukah invested a total of $4350 in
two bonds. He invested in one bond at an annual interest rate of 6% and in another bond at an annual
interest rate of 8%. After one year, the total interest earned was $324.00. How much money did
Tanukah invest in each bond?
a. | $3150 at 6%,
$1200 at 8% | b. | $1200 at 6%,
$3150 at 8%
| c. | $3650 at 6%,
$700 at 8% | d. | $700 at 6%,
$3650 at 8%
|
|
|
|
13.
|
Use an elimination strategy to solve this linear system. 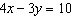 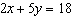
|
|
|
14.
|
Use an elimination strategy to solve this linear system. 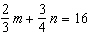 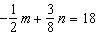
|
|
|
15.
|
Model this situation with a linear system:
Nate borrowed $10 000 for his
university tuition. He borrowed part of the money at an annual interest rate of 2.4% and the rest of
the money at an annual interest rate of 4.5%. His total annual interest payment is $250.50.
|
|
|
16.
|
Without graphing, determine the slope of the graph of the equation:
3x +
4y = 11
a. | 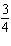 | b. | –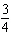 | c. | 4 | d. | 3 |
|
|
|
17.
|
Determine the number of solutions of the linear system:
14x +
7y = 315
16x – 2y = 610
a. | no solution | c. | two solutions | b. | one solution | d. | infinite
solutions |
|
|
|
18.
|
Determine the number of solutions of the linear system:
5x + 7y
= 76
–25x – 35y = –380
a. | 2 solutions | c. | infinite solutions | b. | one solution | d. | no solution |
|
|
|
19.
|
Determine the number of solutions for the linear system that models this
problem:
Two people are playing a game. The difference in their points is 83. When the number
of points each player has is doubled, the difference is 166. How many points does each person
have?
a. | one solution | c. | no solution | b. | two solutions | d. | infinite
solutions |
|
|
|
20.
|
For what value of k does the linear system below have infinite
solutions? 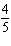 x + y = x + y = 14 kx + 2 y = 28 a. | 28 | b. | 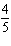 | c. | 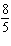 | d. | 0 |
|
Short Answer
|
|
|
21.
|
Create a linear system to model this situation:
The cost of admission to the
museum is $5.50 for adults and $3.50 for students.
Yesterday, 100 admissions were sold, and the
receipts were $424.00.
|
|
|
22.
|
a) Write a linear system to model this
situation: Angela is 24 years older than her cousin Zack. In 13
years, she will be double his age.
b) Use a graph to
solve this problem: How old are Angela and Zack now?
|
|
|
23.
|
Create a linear system to model this situation. Then use substitution to solve
the linear system to solve the problem.
At the local fair, the admission fee is $8.00 for an
adult and $4.50 for a youth. One Saturday, 209 admissions were purchased, with total receipts of
$1304.50. How many adult admissions and how many youth admissions were purchased?
|
|
|
24.
|
Use an elimination strategy to solve this linear system. 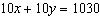 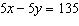
|
|
|
25.
|
Determine the number of solutions of this linear system.
7x –
3y = 43
7x – 3y = 13
|
Problem
|
|
|
26.
|
a) Write a linear system to model this
situation. Mrs. Cheechoo paid $155 for one-day tickets to
Silverwood Theme Park for herself, her husband, and 3 children. Next month, she paid $285 for
herself, 3 adults, and 5 children.
b) Use a graph to
solve this problem: What are the prices of a one-day ticket for an
adult and for a child?
|
|
|
27.
|
a) Use graphing technology to determine
the solution of this linear system. 17x + 10y =
9
7x – 6y = 29
b) Verify the
solution.
|
|
|
28.
|
a) Write a linear system to model this
situation: A large tree removes 1.5 kg of pollution from the air
each year. A small tree removes 0.04 kg each year. An urban forest has 1650 large and small trees.
Together, these trees remove 1818 kg of pollution each year.
b)
Use graphing technology to solve this problem: How many of each size of tree are in the
forest?
c) Verify the solution.
|
|
|
29.
|
Use an elimination strategy to solve this linear
system. Verify the solution.
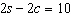 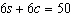
|
|
|
30.
|
Explain what happens when you try to solve this linear system using an
elimination strategy. What does this tell you about the graphs of these equations? 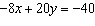 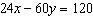
|