Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Car A left Calgary at 8 A.M. to travel 500 mi. to Regina, at an average speed of
63 mph. Car B left Regina at the same time to travel to Calgary at an average speed of 37
mph. A linear system that models this situation is: d = 500 – 63 t
d = 37 t,
where d is the distance in miles from Regina, and t is
the time in hours since 8 A.M. Which graph would you use to determine how far the cars are from
Regina when they meet? What is this distance? a. | Graph C:
195.8 mi. | b. | Graph D:
200 mi. | c. | Graph A:
185 mi. | d. | Graph B:
92.5
mi. |
|
|
|
2.
|
Two life insurance companies determine their premiums using different
formulas: Company A: p = 2 a + 24 Company B: p = 2.25 a + 13, where
p represents the annual premium, and a represents the client’s age. Use the
graph to determine the age at which both companies charge the same premium. 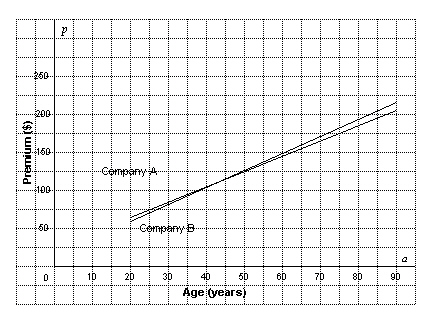 a. | 62 years | b. | 24 years | c. | 59 years | d. | 44 years
|
|
|
|
3.
|
Use the graph to approximate the solution of this linear system: 6 x
– 7 y = –4
– 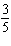 y y = 3 x + 7 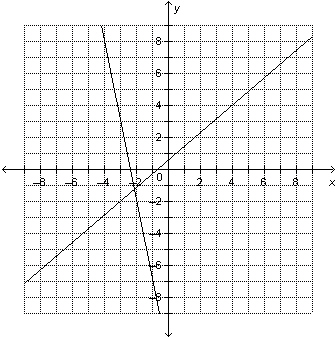 a. | (–0.1, 3.8) | b. | (–2.1, –1.2) | c. | (–1.2, 3.8) | d. | (–2.1,
–0.1) |
|
|
|
4.
|
Express each equation in slope-intercept form. x + 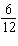 y = y =
–83 12 x + 4 y = –1772
|
|
|
5.
|
For each equation, identify a number you could multiply each term by to ensure
that the coefficients of the variables and the constant term are
integers. (1) 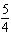 x x + 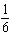 y y = 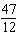 (2)
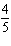 x x – 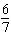 y y = 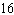 a. | Multiply equation (1) by 35; multiply equation (2) by 12. | b. | Multiply equation
(1) by 12; multiply equation (2) by 35. | c. | Multiply equation (1) by 2; multiply equation
(2) by 3. | d. | Multiply equation (1) by 3; multiply equation (2) by
2. |
|
|
|
6.
|
Create a linear system to model this situation:
A woman is 3 times as old as
her son. In thirteen years, she will be 2 times as old as her son will be.
a. | w = s + 3
w + 13 = 2s | c. | w = 3s
w =
2s | b. | w = 3s
w + 13 = 2(s + 13) | d. | w = 3s
s + 13 =
2(w + 13) |
|
|
|
7.
|
Create a linear system to model this situation:
Tickets for a school play
cost $8 for adults and $4.75 for students.
There were ten more student tickets sold than adult
tickets, and a total of $1399 in ticket sales was collected.
a. | 8a + 4.75s = 1399
s = a + 10 | c. | 8a +
4.75s = 1399
a = s + 10 | b. | 8a + 4.75s = 1399
a +
s = 10 | d. | 4.75a
+ 8s = 1399
s = a + 10 |
|
|
|
8.
|
Yoshiko used this linear system to represent a situation involving the costs of
shirts and pants. 3 s + p = 144 4 s + 3 p = 122 What problem might
Yoshiko have solved? A. Three shirts and one pair of
pants cost $144. Four shirts and three pairs of pants cost $122. Determine the costs of one shirt and one pair
of pants.
B. Three shirts and one pair of pants cost
$144. Two shirts and three pairs of pants cost $122. Determine the costs of one shirt and one pair
of pants.
C. Three shirts cost $144. Four shirts and
three pairs of pants cost $122.
Determine the costs of one shirt and one pair of pants.
D.
Three shirts and 4 pairs of pants cost $144. Four shirts and three
pairs of pants cost $122. Determine
the costs of one shirt and one pair of pants.
a. | Problem D | b. | Problem A | c. | Problem C | d. | Problem
B |
|
|
|
9.
|
Which linear system is represented by this graph? a) 2x –
5y = –16
x =
1
b) 2x + 5y = 16
2x – 5y =
16
c) 2x – 5y = 16
x – 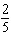 y = y =
–1
d) 2x + 5y = 16
x = –1
| 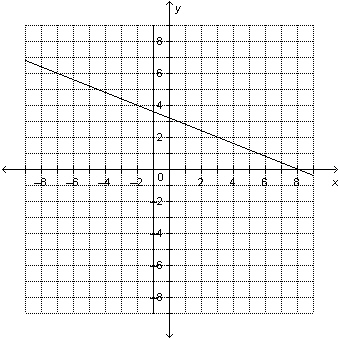 | | |
a. | System a | b. | System d | c. | System b | d. | System
c |
|
|
|
10.
|
Determine the solution of the linear system represented by this graph. a) (2, 3.8)
b) (3.8, 2)
c)
(–3, 3.8)
d) (–2, 3.8) | 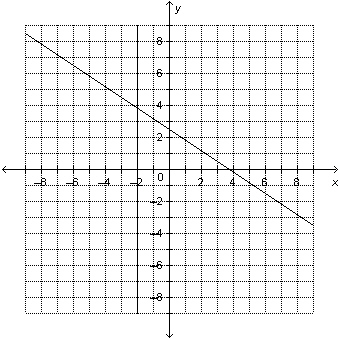 | | |
|
|
|
11.
|
Determine the solution of the linear system represented by this graph. a) (3, 5.3)
b) (5.3, 3)
c) (
5.3, –3)
d) (–4, 5.3)
| 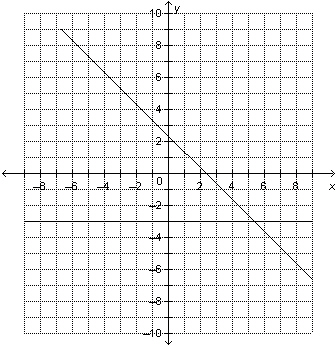 | | |
|
|
|
12.
|
Use substitution to solve this linear system. y = 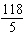 –
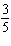 x x13 x + 5 y = 178 a. | (6, –20) | b. | (6, 20) | c. | (–6,
–20) | d. | (–6, 20) |
|
|
|
13.
|
Use substitution to solve this problem:
Tanukah invested a total of $4350 in
two bonds. He invested in one bond at an annual interest rate of 6% and in another bond at an annual
interest rate of 8%. After one year, the total interest earned was $324.00. How much money did
Tanukah invest in each bond?
a. | $3150 at 6%,
$1200 at 8% | b. | $1200 at 6%,
$3150 at 8%
| c. | $3650 at 6%,
$700 at 8% | d. | $700 at 6%,
$3650 at 8%
|
|
|
|
14.
|
Use an elimination strategy to solve this linear system. 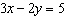 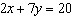
|
|
|
15.
|
Use an elimination strategy to solve this linear system. 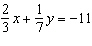 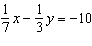
|
|
|
16.
|
Which linear system is modelled by these balance scales? (Each small square on
the right side of the balance scales represents 2 kg.) 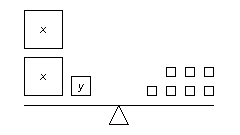 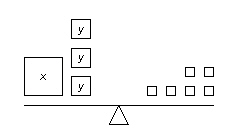
|
|
|
17.
|
Model this situation with a linear system:
Nate borrowed $10 000 for his
university tuition. He borrowed part of the money at an annual interest rate of 2.4% and the rest of
the money at an annual interest rate of 4.5%. His total annual interest payment is $250.50.
|
|
|
18.
|
Determine the number of solutions of the linear system:
14x +
7y = 315
16x – 2y = 610
a. | no solution | c. | two solutions | b. | one solution | d. | infinite
solutions |
|
|
|
19.
|
Determine the number of solutions of the linear system:
5x + 7y
= 76
–25x – 35y = –380
a. | 2 solutions | c. | infinite solutions | b. | one solution | d. | no solution |
|
|
|
20.
|
Determine the number of solutions for the linear system that models this
problem:
Two people are playing a game. The difference in their points is 83. When the number
of points each player has is doubled, the difference is 166. How many points does each person
have?
a. | one solution | c. | no solution | b. | two solutions | d. | infinite
solutions |
|
Short Answer
|
|
|
21.
|
Create a linear system to model this situation:
Two ships start sailing
towards each other at the same time from two islands that are 365 km apart. One ship travels 5 km/h
faster than the other. They meet in 5 h. What is the average speed of each ship?
Verify that 34
km/h and 39 km/h represent the solution of the linear system.
|
|
|
22.
|
A submarine cruises underwater at 20 km/h and on the surface at 30 km/h. The
submarine travels a distance of 650 km in 25 h. A linear system that models this situation
is: u + s = 25 20 u + 30 s = 650 where u represents the
time in hours cruising underwater, and s represents the time in hours cruising on the
surface. a) Graph the linear system above. b)
Use the graph to solve the problem: How long did the submarine travel underwater, and how long did it travel on
the surface?
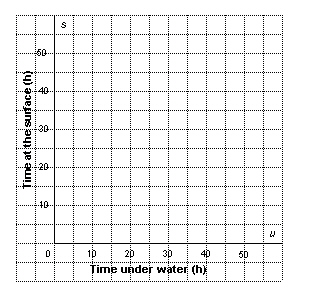
|
|
|
23.
|
Use graphing technology to solve this linear system. Where necessary, write
the coordinates to the nearest tenth. x + 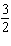 y y = –3 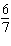 x x +
7 y = –8
|
|
|
24.
|
Create a linear system to model this situation. Then use substitution to solve
the linear system to solve the problem.
At the local fair, the admission fee is $8.00 for an
adult and $4.50 for a youth. One Saturday, 209 admissions were purchased, with total receipts of
$1304.50. How many adult admissions and how many youth admissions were purchased?
|
|
|
25.
|
Use an elimination strategy to solve this linear system. 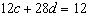 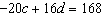
|
Problem
|
|
|
26.
|
a) Write a linear system to model the
situation: A sports club charges an initiation fee and a monthly
fee. At the end of 5 months, a member had paid a total of $450. At the end of 10 months, she had paid
a total of $500.
b) Solve the linear
system by substitution to solve the related problem: What are the
initiation fee and the monthly fee?
|
|
|
27.
|
Use an elimination strategy to solve this linear
system. Verify the solution.
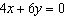 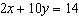
|
|
|
28.
|
a) Model this
situation with a linear system:
To rent a car, a person is
charged a daily rate and a fee for each kilometre driven. When Chena rented a car for 15 days and
drove 800 km, the charge was $715.00. When she rented the same car for 25 days and drove 2250 km, the
charge was $1512.50.
b)
Determine the daily rate and the fee for each kilometre driven. Verify the solution.
|
|
|
29.
|
Use an elimination strategy to solve this linear
system. Verify the solution.
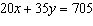 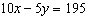
|
|
|
30.
|
Determine the number of solutions of this linear system. 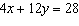 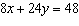
|