Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Which linear system has the solution x = 8 and y = 2.5?
a. | 2x + 2y = 21
2x – 2y = 11 | c. | 2x +
2y = 8
x – y = 21 | b. | x + 2y = 8
2x –
4y = 16 | d. | x + 3y = 22
2x – y =
10 |
|
|
|
2.
|
Which graph represents the solution of the linear system: y =
–2 x 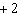 y + y + 6 = 2 x
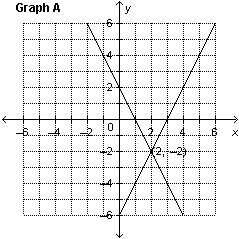 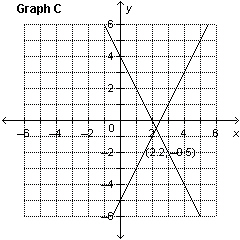  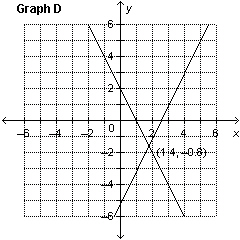 a. | Graph B | c. | Graph C | b. | Graph A | d. | Graph D |
|
|
|
3.
|
a. | (–3, 0.2) | c. | (0.2, –3) | b. | (0, –2.8) | d. | (–2.8, 0) |
|
|
|
4.
|
Car A left Calgary at 8 A.M. to travel 500 mi. to Regina, at an average speed of
63 mph. Car B left Regina at the same time to travel to Calgary at an average speed of 37
mph. A linear system that models this situation is: d = 500 – 63 t
d = 37 t,
where d is the distance in miles from Regina, and t is
the time in hours since 8 A.M. Which graph would you use to determine how far the cars are from
Regina when they meet? What is this distance? a. | Graph C:
195.8 mi. | b. | Graph D:
200 mi. | c. | Graph A:
185 mi. | d. | Graph B:
92.5
mi. |
|
|
|
5.
|
Two life insurance companies determine their premiums using different
formulas: Company A: p = 2 a + 24 Company B: p = 2.25 a + 13, where
p represents the annual premium, and a represents the client’s age. Use the
graph to determine the age at which both companies charge the same premium. 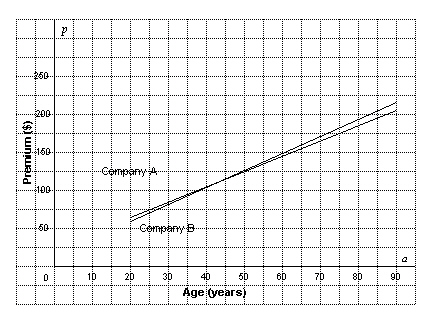 a. | 62 years | b. | 24 years | c. | 59 years | d. | 44 years
|
|
|
|
6.
|
Create a linear system to model this situation:
A woman is 3 times as old as
her son. In thirteen years, she will be 2 times as old as her son will be.
a. | w = s + 3
w + 13 = 2s | c. | w = 3s
w =
2s | b. | w = 3s
w + 13 = 2(s + 13) | d. | w = 3s
s + 13 =
2(w + 13) |
|
|
|
7.
|
Create a linear system to model this situation:
Tickets for a school play
cost $8 for adults and $4.75 for students.
There were ten more student tickets sold than adult
tickets, and a total of $1399 in ticket sales was collected.
a. | 8a + 4.75s = 1399
s = a + 10 | c. | 8a +
4.75s = 1399
a = s + 10 | b. | 8a + 4.75s = 1399
a +
s = 10 | d. | 4.75a
+ 8s = 1399
s = a + 10 |
|
|
|
8.
|
Write a linear system to model this situation. Then verify which of the given
solutions is correct. A crate of 32 grapefruit has a total mass of 4.648 kg. When 9 grapefruit
are removed, the total mass is 3.622 kg. Verify the mass of the crate and the average mass of one
grapefruit. A. 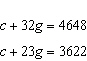 B. B. 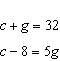 C. C. 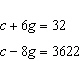 D. D. 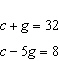 i) i)
The crate has a mass of 1 kg, and the mass of one grapefruit is
114 g. ii) The crate has a mass of 1.2 kg, and the
mass of one grapefruit is 114.2 g. iii) The crate has a mass
of 1 kg, and the mass of one grapefruit is 114.2 g. iv)
The crate has a mass of 1.2 kg, and the mass of one grapefruit is 57 g. a. | Part A-i | c. | Part B-iii | b. | Part C-ii | d. | Part D-iv |
|
|
|
9.
|
Use the graph to solve the linear system: y = –3 x –
5 y 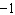 = 3 x 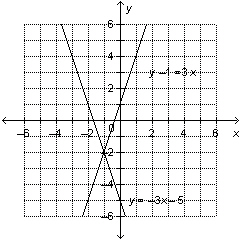 a. | (1, –2) | c. | (1, 0) | b. | (–1, 0) | d. | (–1,
–2) |
|
|
|
10.
|
Which linear system is represented by this graph? a) x –
y = 3
6x + 5y =
14
b) x + y = 5
6x + 5y = 14
c)
x + y = 7
7x
+ 5y = 14
d) x + y
= 9
5x + 6y = 14 | 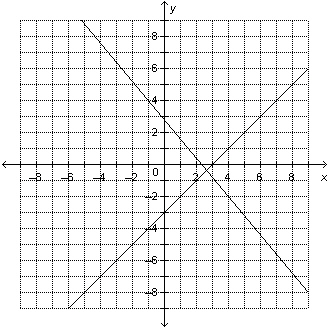 | | |
a. | System a | b. | System b | c. | System c | d. | System
d |
|
|
|
11.
|
Determine the solution of the linear system represented by this graph. a) (2, 3.8)
b) (3.8, 2)
c)
(–3, 3.8)
d) (–2, 3.8) | 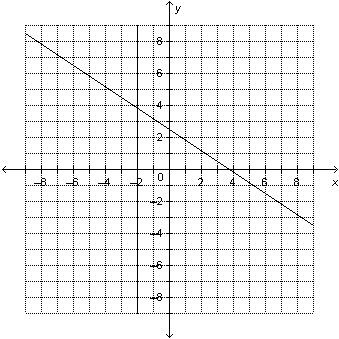 | | |
|
|
|
12.
|
Use substitution to solve this linear system. y = 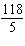 –
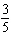 x x13 x + 5 y = 178 a. | (6, –20) | b. | (6, 20) | c. | (–6,
–20) | d. | (–6, 20) |
|
|
|
13.
|
Use substitution to solve this linear system: x – y =
18 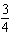 x x + 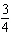 y y = 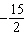 a. | x = 4; y = 18 | b. | x = –14; y =
–14 | c. | x = 4; y = –14 | d. | x = 4; y =
4 |
|
|
|
14.
|
The solution of this linear system is (–3, y). Determine the value
of y. x – 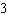 y = y = 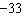
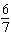 x – y
= x – y
= 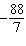
|
|
|
15.
|
The solution of this linear system is (–28, y). Determine the value
of y.
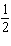 x – x – 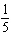 y = y = 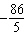
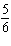 x – x – 4 y = 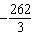
|
|
|
16.
|
Use an elimination strategy to solve this linear system. 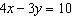 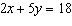
|
|
|
17.
|
Use an elimination strategy to solve this linear system. 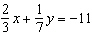 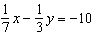
|
|
|
18.
|
Which linear system is modelled by these balance scales? (Each small square on
the right side of the balance scales represents 2 kg.) 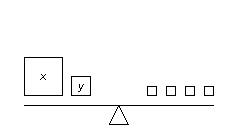 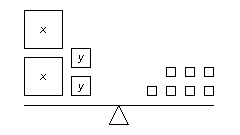
|
|
|
19.
|
Without graphing, determine which of these equations represent parallel
lines.
i) –6x + 6y = 12
ii) –4x + 6y =
12
iii) –2x + 6y = 12
iv) –6x + 6y =
14
a. | ii and iii | b. | i and ii | c. | i and iv | d. | i and
iii |
|
|
|
20.
|
Determine the number of solutions of the linear system:
14x –
5y = 123
14x – 5y = 73
a. | no solution | c. | two solutions | b. | infinite solutions | d. | one solution |
|
Short Answer
|
|
|
21.
|
A submarine cruises underwater at 20 km/h and on the surface at 30 km/h. The
submarine travels a distance of 650 km in 25 h. A linear system that models this situation
is: u + s = 25 20 u + 30 s = 650 where u represents the
time in hours cruising underwater, and s represents the time in hours cruising on the
surface. a) Graph the linear system above. b)
Use the graph to solve the problem: How long did the submarine travel underwater, and how long did it travel on
the surface?
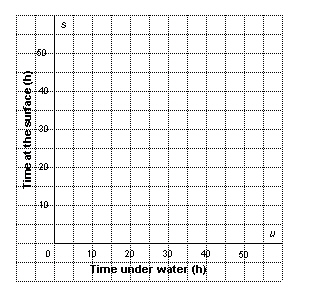
|
|
|
22.
|
a) Write a linear system to model this
situation: A hockey coach bought 25 pucks for a total cost of $70.
The pucks used for practice cost
$2.50 each, and the pucks
used for games cost $3.25 each.
b) Use a graph to
solve this problem: How many of each type of puck did the coach
purchase?
|
|
|
23.
|
Fill in the each blank below with the correct integer. System A
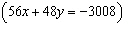 -____: -____:
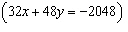 -____: -____: | System B
7x + 6y = –376
–4x –
6y = 256 | | |
|
|
|
24.
|
Use an elimination strategy to solve this linear system. 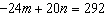 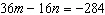
|
|
|
25.
|
The first equation of a linear system is 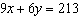 . Write a second equation
to form a linear system with infinite solutions.
|
Problem
|
|
|
26.
|
a) Write a linear system to model this
situation: A large tree removes 1.5 kg of pollution from the air
each year. A small tree removes 0.04 kg each year. An urban forest has 1650 large and small trees.
Together, these trees remove 1818 kg of pollution each year.
b)
Use graphing technology to solve this problem: How many of each size of tree are in the
forest?
c) Verify the solution.
|
|
|
27.
|
a) Write a linear system to model the
situation: A sports club charges an initiation fee and a monthly
fee. At the end of 5 months, a member had paid a total of $450. At the end of 10 months, she had paid
a total of $500.
b) Solve the linear
system by substitution to solve the related problem: What are the
initiation fee and the monthly fee?
|
|
|
28.
|
a) Model this
situation with a linear system:
To rent a car, a person is
charged a daily rate and a fee for each kilometre driven. When Chena rented a car for 15 days and
drove 800 km, the charge was $715.00. When she rented the same car for 25 days and drove 2250 km, the
charge was $1512.50.
b)
Determine the daily rate and the fee for each kilometre driven. Verify the solution.
|
|
|
29.
|
Use the equation 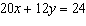 as an equation in three different linear systems. Write a
second equation so that each system has a different number of solutions. Explain what you did for
each system.
|
|
|
30.
|
Determine the number of solutions of this linear system. 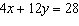 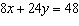
|