Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Which linear system has the solution x = 4 and y =
–2?
a. | x + 4y = 15
4x 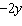 = –17 = –17 | c. | 4x +
y = 14
–2x 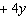 = –16 = –16 | b. | 2x + 4y = 4
–2x
+ y = 14 | d. | x +
4y = 4
2x + 4y = 8 |
|
|
|
2.
|
Express each equation in slope-intercept form. x + 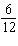 y = y =
–83 12 x + 4 y = –1772
|
|
|
3.
|
Use the table of values to determine the solution of this linear system:
a. | (–2, 2) | c. | (2, 2) | b. | (2,–2) | d. | (–2,
–2) |
|
|
|
4.
|
Write an equivalent linear system where both equations have the same
x-coefficients.  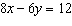
|
|
|
5.
|
The first equation of a linear system is –6x + 12y =
–42. Choose a second equation to form a linear system with no solution.
i)
–6x + 12y = 126 ii) 18x –
36y = 126 iii) 18x + 12y =
126 iv) 18x + 36y = 0
a. | Equation iv | b. | Equation ii | c. | Equation iii | d. | Equation
i |
|
|
|
6.
|
Create a linear system to model this situation:
The perimeter of an isosceles
triangle is 36 cm. The base of the triangle is 9 cm longer than each equal side.
a. | s + b = 36
b – 9 = s | b. | 2s +
b = 36
b + 9 = s | c. | 2b + s = 36
s + 9 = b | d. | 2s + b = 36
s + 9 =
b |
|
|
|
7.
|
Create a linear system to model this situation:
A woman is 3 times as old as
her son. In thirteen years, she will be 2 times as old as her son will be.
a. | w = s + 3
w + 13 = 2s | c. | w = 3s
w =
2s | b. | w = 3s
w + 13 = 2(s + 13) | d. | w = 3s
s + 13 =
2(w + 13) |
|
|
|
8.
|
Create a linear system to model this situation:
A rectangular field is 35 m
longer than it is wide. The length of the fence around
the perimeter of the field is 290
m.
a. | l + 35 = w
2l + 2w = 290 | b. | l = w
+ 35
2l + 2w = 290 | c. | l = w + 35
l + w =
290 | d. | l = w + 35
lw = 290 |
|
|
|
9.
|
Write a linear system to model this situation. Then verify which of the given
solutions is correct. A crate of 32 grapefruit has a total mass of 4.648 kg. When 9 grapefruit
are removed, the total mass is 3.622 kg. Verify the mass of the crate and the average mass of one
grapefruit. A. 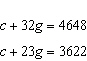 B. B. 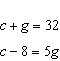 C. C. 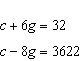 D. D. 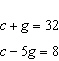 i) i)
The crate has a mass of 1 kg, and the mass of one grapefruit is
114 g. ii) The crate has a mass of 1.2 kg, and the
mass of one grapefruit is 114.2 g. iii) The crate has a mass
of 1 kg, and the mass of one grapefruit is 114.2 g. iv)
The crate has a mass of 1.2 kg, and the mass of one grapefruit is 57 g. a. | Part A-i | c. | Part B-iii | b. | Part C-ii | d. | Part D-iv |
|
|
|
10.
|
Which linear system is represented by this graph? a) x –
y = 5
5x + 6y =
18
b) x – y =
7
5x + 6y = 18
c)
x – y = 9
6x + 6y =
18
d) x – y = 11
6x + 5y = 18 | 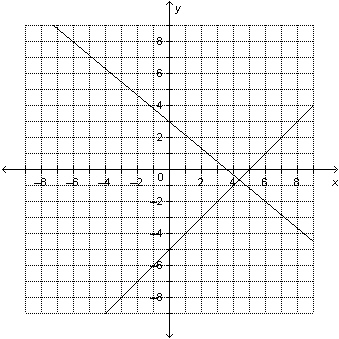 | | |
a. | System d | b. | System b | c. | System a | d. | System
c |
|
|
|
11.
|
Determine the solution of the linear system represented by this graph. a) (3, 5.3)
b) (5.3, 3)
c) (
5.3, –3)
d) (–4, 5.3)
| 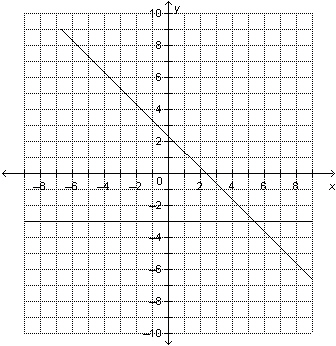 | | |
|
|
|
12.
|
Use substitution to solve this problem:
The perimeter of a rectangular field
is 276 m. The length is 18 m longer than the width.
What are the dimensions of the
field?
a. | 58 m by 80 m | b. | 68 m by 70 m | c. | 78 m by 60 m | d. | 48 m by 90 m
|
|
|
|
13.
|
Use an elimination strategy to solve this linear system. 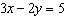 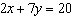
|
|
|
14.
|
Model this situation with a linear system:
Frieda has a 13% silver alloy and
a 31% silver alloy. Frieda wants to make 26 kg of an alloy that is 47% silver.
|
|
|
15.
|
Model this situation with a linear system:
At a campground, 5 large tanks and
5 small tanks contained 3200 L of drinking water. When one of the small tanks was replaced with a
large tank, there was 3400 L of drinking water.
|
|
|
16.
|
Use an elimination strategy to solve this linear system. 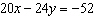 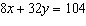
|
|
|
17.
|
Model this situation with a linear system:
Nate borrowed $10 000 for his
university tuition. He borrowed part of the money at an annual interest rate of 2.4% and the rest of
the money at an annual interest rate of 4.5%. His total annual interest payment is $250.50.
|
|
|
18.
|
Without graphing, determine the slope of the graph of the equation:
3x +
4y = 11
a. | 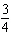 | b. | –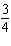 | c. | 4 | d. | 3 |
|
|
|
19.
|
Determine the number of solutions of the linear system:
2x –
5y = 23
–6x + 15y = 21
a. | one solution | c. | two solutions | b. | no solution | d. | infinite
solutions |
|
|
|
20.
|
Two lines in a linear system have the same slope, but different
y-intercepts.
How many solutions does the linear system have?
a. | two solutions | c. | infinite solutions | b. | no solution | d. | one solution |
|
Short Answer
|
|
|
21.
|
Solve this linear system by graphing. –3 x – 2 y =
16 – x + y = –8 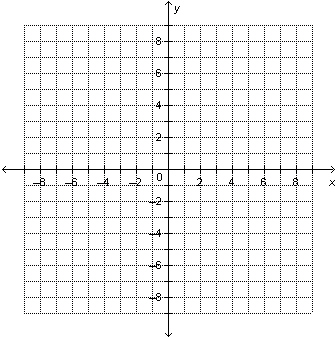
|
|
|
22.
|
Solve this linear system by graphing. y = –8
–3 x + y = 7 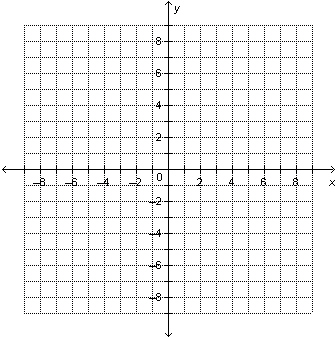
|
|
|
23.
|
Use graphing technology to solve this linear system.
Where necessary, write
the coordinates to the nearest tenth.
–3x + 4y = –3
5x +
6y = –5
|
|
|
24.
|
Identify two like terms and say how they are related.
6x + 4y =
–258
–3x + 5y = 45
|
|
|
25.
|
For what values of k does the linear system below
have: a) infinite
solutions? b) one solution? c)
no solution? 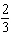 x x + y
= 16 kx + 3 y = 48
|
Problem
|
|
|
26.
|
In a piggy bank, the number of nickels is 8 more than one-half the number of
quarters. The value of the coins is $21.85.
a) Create a
linear system to model the situation.
b) If the number of
quarters is 78, determine the number of nickels.
|
|
|
27.
|
These balance scales illustrate the two different sizes of cartons of detergent:
x represents the mass of a large carton and y represents the mass of a small
carton. 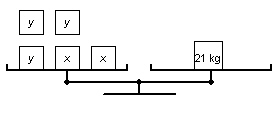 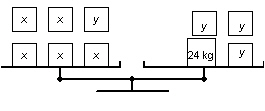 a) a)
Write a linear system to model the two balance scales. b) Use the diagrams of the balance
scales to verify that a large carton of detergent has a mass of 6 kg and a small carton has a mass of
3 kg.
c) Use the linear system to verify the masses of
the cartons in part b.
|
|
|
28.
|
a) Write a linear system whose solution
is: x = 5, y = –5.
b) Is there more than
one linear system with this solution? Explain.
|
|
|
29.
|
a) Write a linear system to model the
situation: A sports club charges an initiation fee and a monthly
fee. At the end of 5 months, a member had paid a total of $450. At the end of 10 months, she had paid
a total of $500.
b) Solve the linear
system by substitution to solve the related problem: What are the
initiation fee and the monthly fee?
|
|
|
30.
|
Use a substitution strategy to solve the following problem.
Two isosceles
triangles have the same base length. The equal sides of one of the triangles
are 3.25 times as
long as the equal sides of the other. Find the lengths of the sides of the triangles when their
perimeters are 38 cm and 96.5 cm.
|