Math 12 Practice Quiz #2

Name:

Multiple Choice
Identify the choice that best completes the statement or answers the question.

Compared to the graph of the base function , the graph of the function

is translated

A	9 units to the left	C	9 units down
B	9 units to the right	D	9 units up

Given the graph of f(x) shown below, what are the coordinates of point A if the transformed graph is represented by

A		C
B		D

Given the graph of f(x) shown below, what are the coordinates of point A if the transformed graph is represented by

A		C
B		D

The function

represents a transformation that can best be described as

A	a reflection in the x-axis	C	a reflection in the y-axis
B	a reflection in the x-axis and the y-axis	D	a reflection in the line y = x

When b > 0, the function has what relationship to the base function

A	f(x) is stretched vertically by a factor of \|b\| and reflected in the x-axis
B	f(x) is stretched vertically by a factor of \|b\|
C	f(x) is stretched horizontally by a factor of 1/\|b\| and reflected in the y-axis
D	f(x) is stretched horizontally by a factor of 1/\|b\|

Short Answer

a) Sketch the graph of

for each base function.
i)

ii)

iii)

b) Write the equation for g(x) to represent a single stretch that results in the same graph as in each function in part a).
c) Describe how each stretch affects the domain and range for each function.

Problem

The graph of

is transformed to the graph of

.
a) Describe the two translations represented by this transformation.
b) Determine three points on the base function. Horizontally translate and then vertically translate the points. What are the three resulting image points?

For the base function

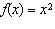
, a reflection in the y-axis is followed by a reflection in the x-axis.
a) Discuss the effect of each reflection on the base function.
b) Is there a point that you expect to be invariant during these reflections? If so, state its coordinates.
c) Graph the function after each reflection.
d) Use your graph in part c) to verify your answer for part b).
e) Make a general statement regarding invariant points after reflections in the x-axis and the y-axis.