Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Which set of properties is correct for the function 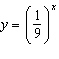 ?
|
|
|
2.
|
The equation 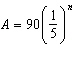 can also be written as
|
|
|
3.
|
Which of the following transformations maps the function 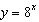 onto the
function 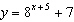 ? A | a horizontal shift of 5 units to the left and a vertical shift of 7 units
up | B | a horizontal shift of 5 units to the right and a vertical shift of 7 units
down | C | a horizontal shift of 5 units to the right and a vertical shift of 7 units
up | D | a horizontal shift of 5 units to the left and a vertical shift of 7 units
down |
|
|
|
4.
|
Which function results when the graph of 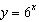 is translated 2 units
down?
|
|
|
5.
|
Which equation can be used to model the given information, where the population
has been rounded to the nearest whole number? Year (x) | Population
(y) | 0 | 100 | 1 | 104 | 2 | 108 | 3 | 112 | 4 | 117 | 5 | 122 | | |
|
|
|
6.
|
A radioactive sample with an initial mass of 1 mg has a half-life of 9 days.
What is the equation that models the exponential decay, A, for time, t, in 9-day
intervals?
|
|
|
7.
|
A colony of ants has an initial population of 750 and triples every day. Which
function can be used to model the ant population, p, after t days?
|
|
|
8.
|
An investment of $150 is placed into an account that earns interest, compounded
annually, at a rate of 5% for 12 years. The amount, A, in the account can be modelled by the
function 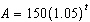 , where t is the time, in years. What is the domain of this function?
|
|
|
9.
|
Jennifer deposited some money into an account that pays 7% per year, compounded
annually. Today her balance is $300. How much was in the account 10 years ago, to the nearest
cent? [Hint: Use 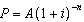 .] A | $163.18 | C | $42.86 | B | $30.00 | D | $152.50 |
|
|
|
10.
|
The population of a bacterial culture triples every hour. When the scientist
observed the culture, it had already been growing for some time. She developed the equation for the
population, P, after t hours as 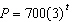 , based on t = 0 representing the
time she started her measurements. How many bacterial cells were there 2 h before she started
measuring?
|
Short Answer
|
|
|
1.
|
a) Determine the type of function shown in each graph. i)
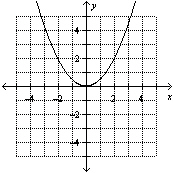 ii) ii) 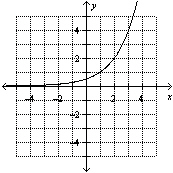 iii) iii) 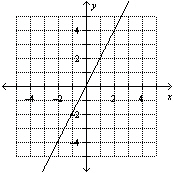 b) b) Describe what
you would expect to see in the first differences column of a table of values for each graph in part
a).
|
|
|
2.
|
Sketch the graph of an exponential function with all of the following
characteristics: • domain 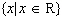 • • range 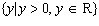 •
y •
y-intercept of 3 • no x-intercept • the function is
always decreasing
|
|
|
3.
|
Write the equation for the function that results from each transformation or set
of transformations applied to the base function 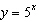 . a) reflect in the
y-axis b) shift 3 units to the right c) shift 1 unit down and 4 units to
the left d) reflect in the x-axis and shift 2 units down
|
Problem
|
|
|
1.
|
When interest is compounded semi-annually, the formula used to find the amount
of an investment is 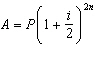 , where A represents the amount; P represents
the principal invested; i represents the annual interest rate, as a decimal; and n
represents the number of years of the investment. a) Use the formula to determine the
amount that each investment would be worth. i) $5000 at a rate of 4%, compounded
semi-annually, for 10 years ii) $4000 at a rate of 5%, compounded semi-annually, for 20
years b) If interest is compounded quarterly, the formula becomes 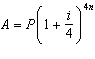 . Use the
formula to determine the amount that the investments from part a) would be worth if interest were
compounded quarterly. c) Explain the difference in the answers for parts a) and b).
|
|
|
2.
|
A $21 500 investment earns 5.25% interest, compounded quarterly.
a)
Determine the value of the investment in 5 years.
b) How long will it take the original
investment to double in value?
|