Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Which set of properties is correct for the function 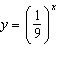 ?
|
|
|
2.
|
Which function results when the graph of the function 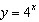 is reflected
in the y-axis, compressed vertically by a factor of 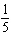 , and shifted 2 units down?
|
|
|
3.
|
What is the exponential equation for the function that results from the
transformations listed being applied to the base function 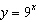 ? •
a reflection in the y-axis
• a vertical stretch by a factor of 6
• a
horizontal stretch by a factor of 7
|
|
|
4.
|
Which equation can be used to model the given information, where the population
has been rounded to the nearest whole number? Year (x) | Population
(y) | 0 | 100 | 1 | 104 | 2 | 108 | 3 | 112 | 4 | 117 | 5 | 122 | | |
|
|
|
5.
|
Solve for x.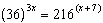
|
|
|
6.
|
A colony of ants has an initial population of 900 and doubles every day. Which
function can be used to model the ant population, p, after t days?
|
|
|
7.
|
A bacteria colony initially has 5500 cells and triples every week. Which
function can be used to model the population, p, of the colony after t days?
|
|
|
8.
|
An investment of $300 is placed into an account that earns interest, compounded
annually, at a rate of 4% for 6 years. The amount, A, in the account can be modelled by the
function 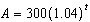 , where t is the time, in years. What is the domain of this function?
|
|
|
9.
|
A rumour is being spread in a community that the mayor is going to retire before
the next election. Initially, 5 people were told the rumour and each of these people told 5 others
the following day. Each of the 5 people told by the initial people told 5 others the day after they
were told. If this process keeps up, how many people will be told the rumour on the fifth day?
A | 625 people | C | 25 people | B | 15 625 people | D | 3125 people |
|
|
|
10.
|
To the nearest year, how long would an investment need to be left in the bank at
4%, compounded annually, for the investment to quadruple?
A | 35 years | C | 16 years | B | 47 years | D | 39 years |
|
Short Answer
|
|
|
1.
|
Solve for n: 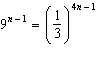
|
|
|
2.
|
Solve for x: 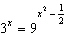
|
|
|
3.
|
Graphically solve the system 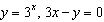 . 
|
Problem
|
|
|
1.
|
A colony of ants starts with an initial population of 50 and doubles every week
for 8 weeks.
a) Create a table of values for weeks 0 to 8 for the population of the
colony.
b) Graph the data from your table of values.
c) Is the relationship
between the ant population and the number of weeks exponential? Explain.
d) Model the
information using an equation.
|
|
|
2.
|
The table shows the value, V, of Rachel’s car t years after
it was purchased. Years After
Purchase |
Value ($)
| 0 | 42 000 | 1 | 37 800 | 2 | 34 020 | 3 | 30 618 | 4 | 27 556 | | |
a) Make a scatter plot for the
data. b) Describe the shape of the curve. c) Determine an equation to model the
data. d) Use the equation to determine the value of the car in 8 years. e)
Approximately how long will it take for the car to be worth less than $10 000?
|