Name: 

Which function results when the graph of is translated 2 units down?

Which graph represents the function ?

Which equation can be used to model the given information, where the population has been rounded to the nearest whole number?

Year (x)	Population (y)
0	100
1	104
2	108
3	112
4	117
5	122

Solve for x.

The half-life of a radioactive element can be modelled by , where is the initial mass of the element; is the elapsed time, in hours; and is the mass that remains after time . The half-life of the element is

A radioactive sample with an initial mass of 1 mg has a half-life of 11 days. What is the equation that models the exponential decay, A, for time, t, in 11-day intervals?

A bacteria colony initially has 6500 cells and triples every week. Which function can be used to model the population, p, of the colony after t days?

An investment of $500 is placed into an account that earns interest, compounded annually, at a rate of 8% for 2 years. The amount, A, in the account can be modelled by the function , where t is the time, in years. What is the domain of this function?

Mohamed purchased a car for $34 000. It depreciates by 20% of its current value every year. How much will the car be worth 3 years after it is purchased?

Solve for x.

Sketch an exponential function with all of the given conditions:
• domain
• range
• y-intercept of –4
• no x-intercept
• the function is always increasing

Write the equation for the function that results from each transformation or set of transformations applied to the base function .
a) reflect in the y-axis
b) shift 3 units to the right
c) shift 1 unit down and 4 units to the left
d) reflect in the x-axis and shift 2 units down

Solve for x:

A colony of ants starts with an initial population of 50 and doubles every week for 8 weeks.
a) Create a table of values for weeks 0 to 8 for the population of the colony.
b) Graph the data from your table of values.
c) Is the relationship between the ant population and the number of weeks exponential? Explain.
d) Model the information using an equation.

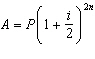
When interest is compounded semi-annually, the formula used to find the amount of an investment is , where A represents the amount; P represents the principal invested; i represents the annual interest rate, as a decimal; and n represents the number of years of the investment.
a) Use the formula to determine the amount that each investment would be worth.
i) $5000 at a rate of 4%, compounded semi-annually, for 10 years
ii) $4000 at a rate of 5%, compounded semi-annually, for 20 years
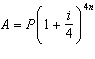
b) If interest is compounded quarterly, the formula becomes . Use the formula to determine the amount that the investments from part a) would be worth if interest were compounded quarterly.
c) Explain the difference in the answers for parts a) and b).