Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Which set of properties does the function 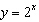 have? A | no x-intercept, no y-intercept | C | no x-intercept,
y-intercept is 1 | B | x-intercept is 1, no
y-intercept | D | x-intercept is 0, y-intercept is 0 |
|
|
|
2.
|
Which choice best describes the function 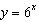 ? A | both increasing and decreasing | C | increasing | B | decreasing | D | neither increasing nor decreasing |
|
|
|
3.
|
The equation 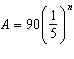 can also be written as
|
|
|
4.
|
For the exponential function 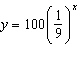 , which of the following statements is
not true? A | The graph of the function is increasing. | B | The graph of the
function is decreasing. | C | The domain is the set of real
numbers. | D | The range is the set of real numbers greater than
zero. |
|
|
|
5.
|
What is the exponential equation for the function that results from the
transformations listed being applied to the base function 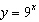 ? •
a reflection in the y-axis
• a vertical stretch by a factor of 6
• a
horizontal stretch by a factor of 7
|
|
|
6.
|
A colony of ants has an initial population of 750 and triples every day. Which
function can be used to model the ant population, p, after t days?
|
|
|
7.
|
An investment of $150 is placed into an account that earns interest, compounded
annually, at a rate of 5% for 12 years. The amount, A, in the account can be modelled by the
function 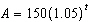 , where t is the time, in years. What is the domain of this function?
|
|
|
8.
|
The population of a bacterial culture triples every hour. When the scientist
observed the culture, it had already been growing for some time. She developed the equation for the
population, P, after t hours as 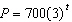 , based on t = 0 representing the
time she started her measurements. How many bacterial cells were there 2 h before she started
measuring?
|
|
|
9.
|
Which of the following represents 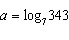 ?
|
|
|
10.
|
Evaluate 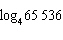 .
|
|
|
11.
|
What is the equation for the asymptote of the function 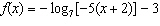 ? A | x = 2 | C | x = –5 | B | x = –3 | D | x =
–2 |
|
|
|
12.
|
If 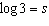 , 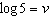 , and 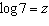 , an algebraic expression
in terms of s, v, and z for 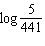 is A | v - 2s + 2z | C | v - 2(s - z) | B | v - 2(s + z) | D | v - 2s
+ z |
|
|
|
13.
|
Evaluate the expression 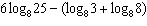 to the nearest hundredth.
|
|
|
14.
|
Solve 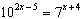 . Round your answer to two decimal places.
|
|
|
15.
|
The eye size of many vertebrates is related to body mass by the logarithmic
equation 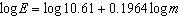 , where E is the eye axial length, in millimetres, and m is the body mass,
in kilograms. Predict the mass of a vertebrate with an eye axial length of 43 mm. Round your answer
to the nearest hundredth of a kilogram. A | 2.66 | C | 1242.98 | B | 868.60 | D | 1.32 |
|
Short Answer
|
|
|
1.
|
|
|
|
2.
|
Sketch an exponential function with all of the given conditions: •
domain 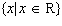 • range 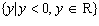 • y-intercept of –4 • no
x-intercept • the function is always increasing
|
|
|
3.
|
Solve for n: 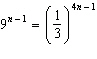
|
|
|
4.
|
Evaluate 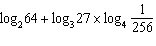 .
|
|
|
5.
|
Solve for x. 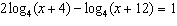
|
Problem
|
|
|
1.
|
a) Write the equation for a transformed exponential function with a base
of 4 that passes through the point 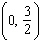 . b) Write two equations, different from the one
in part a), that satisfy these criteria. c) Use algebraic and/or graphical reasoning to
explain why each equation is a solution.
|
|
|
2.
|
The intensity level, 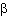 , in decibels, of sound is defined as 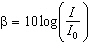 , where
I is the intensity of the sound in watts per square metre.The ratio of the intensity of sound
pollution measured at a small airport runway versus that of the local highway is 6420.4. If the sound
level on the local highway is 91 dB, determine the sound level on the runway, to the nearest
decibel.
|
|
|
3.
|
Explain the steps used to solve the equation 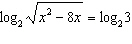 .
|