Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
When a > 0, the function 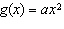 has what relationship to the base
function 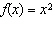 ? A | f(x) is stretched vertically by a factor of |a| and reflected in the
x-axis | B | f(x) is stretched horizontally by a factor of 1/|a| | C | f(x) is
stretched vertically by a factor of |a| | D | f(x) is stretched horizontally by
a factor of 1/|a| and reflected in the y-axis |
|
|
|
2.
|
Which of the graphs shown below represents the base function 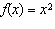 and the
stretched function g( x) = 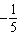 x2 x2?
|
|
|
3.
|
When b < 0, the function 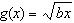 has what relationship to the base
function 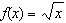 ? A | f(x) is stretched horizontally by a factor of 1/|b| | B | f(x) is
stretched horizontally by a factor of 1/|b| and reflected in the y-axis | C | f(x) is
stretched vertically by a factor of |b| | D | f(x) is stretched vertically by a
factor of |b| and reflected in the x-axis |
|
|
|
4.
|
What is the equation of the transformed function, g( x), after the
transformations are applied to the graph of the base function 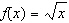 , shown in blue, to
obtain the graph of g( x), shown in red? 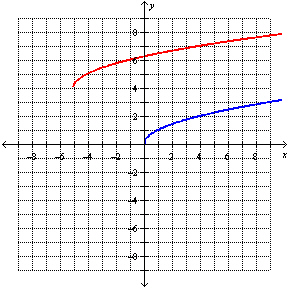
|
|
|
5.
|
What is the solution to the radical equation 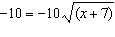 ?
|
|
|
6.
|
What is the restriction on x if 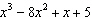 is divided by 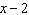 ?
|
|
|
7.
|
What is the remainder when 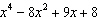 is divided by 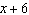 ?
|
|
|
8.
|
One root of the equation 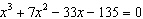 is
|
|
|
9.
|
Based on the graph of 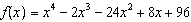 , what are the real roots of 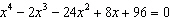 ? 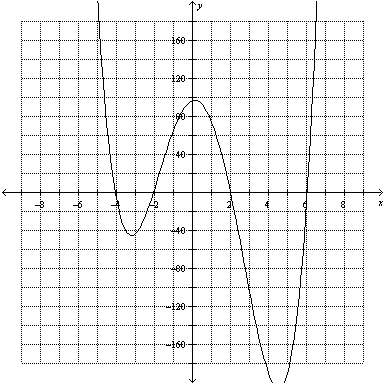 A | –6, –2, 2, 4 | C | there are no real
roots | B | 6, 2, –2, –4 | D | impossible to determine |
|
|
|
10.
|
Determine the equation of a circle with centre at (3, –3) and radius
10.
|
|
|
11.
|
Determine the measure of the angle in standard position shown on the graph
below. Round your answer to the nearest tenth of a degree. A | 161.6° | C | 71.6° | B | 341.6° | D | 251.6° |
|
|
|
12.
|
The coordinates of the point that lies at the intersection of the terminal arm
and the unit circle at an angle of 110° are
A | (0.94, –0.34) | C | (–0.34, 0.94) | B | (–0.34, –2.75) | D | (–2.75,
0.94) |
|
|
|
13.
|
If the angle q is –5000° in standard
position, it can be described as having made
A | 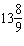 rotations rotations | C | 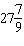 rotations
rotations | B | 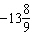 rotations rotations | D | 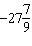 rotations rotations |
|
|
|
14.
|
A ball is riding the waves at a beach. The ball’s up and down motion with
the waves can be described using the formula 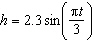 , where h is the height, in metres,
above the flat surface of the water and t is the time, in seconds. What is the height of the
ball, to the nearest hundredth of a metre, after t = 17 s? A | –0.87 m | C | –1.99 m | B | –2.66 m | D | 1.99 m |
|
|
|
15.
|
Determine the point in quadrant II where the line represented by 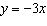 intersects the
unit circle. A | (0.95, –0.32) | C | (–0.35, 0.94) | B | (–0.32, 0.95) | D | (–0.32,
0.94) |
|
|
|
16.
|
Which graph represents the function y = 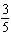 sin (  q) q), where q is in radians?
|
|
|
17.
|
What is the period of the sinusoidal function 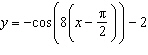 ?
|
|
|
18.
|
Solve 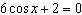 to three decimal places on the interval 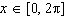 . A | x = 0.340, x = 5.943 | C | x = 1.911, x =
1.231 | B | x = 1.231, x = 5.052 | D | x = 1.911, x =
4.373 |
|
|
|
19.
|
Which equation is a reciprocal identity?
|
|
|
20.
|
What does the expression 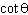 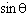 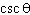 simplify to?
|
|
|
21.
|
Simplify 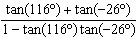 .
|
|
|
22.
|
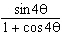 is equivalent to
|
|
|
23.
|
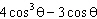 can be rewritten as
|
|
|
24.
|
An investment of $150 is placed into an account that earns interest, compounded
annually, at a rate of 5% for 12 years. The amount, A, in the account can be modelled by the
function 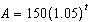 , where t is the time, in years. What is the domain of this function?
|
|
|
25.
|
To the nearest year, how long would an investment need to be left in the bank at
5%, compounded annually, for the investment to triple?
A | 15 years | C | 28 years | B | 26 years | D | 23 years |
|
|
|
26.
|
If 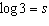 , 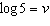 , and 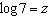 , an algebraic expression
in terms of s, v, and z for 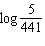 is A | v - 2s + 2z | C | v - 2(s - z) | B | v - 2(s + z) | D | v - 2s
+ z |
|
|
|
27.
|
Solve 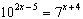 . Round your answer to two decimal places.
|
|
|
28.
|
The eye size of many vertebrates is related to body mass by the logarithmic
equation 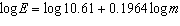 , where E is the eye axial length, in millimetres, and m is the body mass,
in kilograms. Predict the mass of a vertebrate with an eye axial length of 43 mm. Round your answer
to the nearest hundredth of a kilogram. A | 2.66 | C | 1242.98 | B | 868.60 | D | 1.32 |
|
|
|
29.
|
Solve the equation 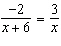 . A | x = 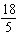 | C | x = 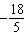 | B | x = 3 | D | x = 4 |
|
|
|
30.
|
Given the functions 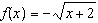 and 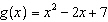 , what is the domain of the combined
function 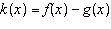 ?
|
|
|
31.
|
What is the value of 6!?
|
|
|
32.
|
Evaluate 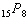 . A | 32 432 400 | C | 6435 | B | 163 459 296 000 | D | 259 459 200 |
|
|
|
33.
|
Jenni and Hari go to a local Chinese restaurant for dim sum. If there are 20
items on the menu, and Jenni orders 7 items and Hari orders 11 items, which expression represents the
total number of choices between them?
|
|
|
34.
|
Determine the coefficient, a, for the term 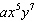 of the binomial expansion
of 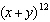 .
|
|
|
35.
|
Prom’s friend gives him a row of Pascal’s triangle and asks which
row it comes from. Prom adds the numbers and obtains a sum of 65 536. Which row do the numbers come
from?
|
Short Answer
|
|
|
1.
|
Solve by graphing using technology. Round answers to one decimal place.
a) x3 – 7 > 0
b) 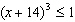
|
|
|
2.
|
A population, p, of bears varies according to 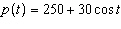 , where
t is the time, in years, and angles are measured in radians. a) What are the maximum
and minimum populations? b) What is the first interval, in years and months, over which the
population is increasing?
|
|
|
3.
|
Determine the value of 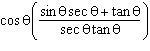 if 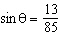 and 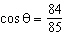 .
|
|
|
4.
|
What is the solution for 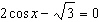 for 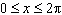 ?
|
|
|
5.
|
Sketch the graph of the function 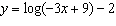 .
|
Problem
|
|
|
1.
|
Create a cubic polynomial inequality for which x = 3 or 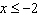
is the solution. Explain your reasoning .
|
|
|
2.
|
a) For the given trigonometric ratio, determine two other angles that
have the same value.
i) sin 45°
ii) tan 300°
iii) cos
120°
b) Explain how you determined the angles in part a).
|
|
|
3.
|
Wilson places a measuring tape on a pillar of a dock to record the water level
in his local coastal community. He finds that a high tide of 1.77 m occurs at 5:17 a.m., and a low
tide of 0.21 m occurs at 11:38 a.m.
a) Estimate the period of the fluctuation of the water
level.
b) Estimate the amplitude of the pattern.
c) Predict when the next two
high tides will occur.
d) Predict when the next two low tides will occur.
|
|
|
4.
|
Solve the equation 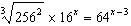 .
|
|
|
5.
|
a) Use the asymptotes and intercepts to make a quick sketch of the
function 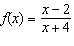 and its reciprocal, 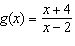 , on the same set of axes. b) Describe the
symmetry in the graphs in part a). c) Determine the equation of the mirror line in your
graph from part a). d) Determine intervals of increase and decrease for both f and
g. How do the sets of intervals compare? e) Does the pattern from part d) occur for
all pairs of functions 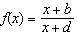 and 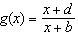 , 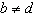 ? Explain why or why
not.
|