Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Compared to the graph of the base function 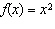 , the graph of the
function 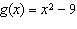 is translated A | 9 units to the left | C | 9 units down | B | 9 units to the right | D | 9 units up |
|
|
|
2.
|
Compared to the graph of the base function 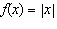 , the graph of the
function 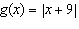 is translated A | 9 units to the right | C | 9 units down | B | 9 units up | D | 9 units to the
left |
|
|
|
3.
|
Which of the graphs shown below represents the base function 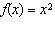 and the
stretched function g( x) = ( 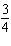 x x) 2?
|
|
|
4.
|
Compared to the graph of the base function 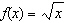 , the graph of the
function 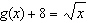 is translated A | 8 units to the left | C | 8 units to the right | B | 8 units up | D | 8 units down |
|
|
|
5.
|
Which graph represents an odd-degree polynomial function with two
x-intercepts?
|
|
|
6.
|
What is the restriction on x if 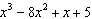 is divided by 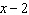 ?
|
|
|
7.
|
What is the remainder when 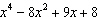 is divided by 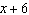 ?
|
|
|
8.
|
Determine the value of k so that 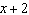 is a factor of 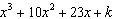 . A | k = –1 | C | k = 14 | B | k = –14 | D | k = 1 |
|
|
|
9.
|
Given the function 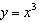 , what are the parameters of the transformed function
y = 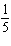 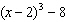 and what is the effect of each parameter
on the graph of the original function? A | a = 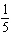 , vertical stretch about the x-axis by a factor of , vertical stretch about the x-axis by a factor of
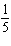
h = –8, horizontal translation 8 units right
k = 2, vertical
translation 2 units down | B | a = 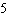 , vertical stretch about
the x-axis by a factor of , vertical stretch about
the x-axis by a factor of 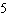
h = 2, horizontal translation 2 units
left
k = –8, vertical translation 8 units right | C | a = 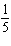 ,
vertical stretch about the x-axis by a factor of ,
vertical stretch about the x-axis by a factor of 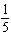
h = 2, horizontal translation
2 units right
k = –8, vertical translation 8 units down | D | a = 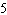 ,
vertical stretch about the x-axis by a factor of ,
vertical stretch about the x-axis by a factor of 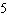
h = 2, horizontal
translation 2 units right
k = –8, vertical translation 8 units
down |
|
|
|
10.
|
The coordinates of the point that lies at the intersection of the terminal arm
and the unit circle at an angle of 110° are
A | (0.94, –0.34) | C | (–0.34, 0.94) | B | (–0.34, –2.75) | D | (–2.75,
0.94) |
|
|
|
11.
|
Identify the point on the unit circle corresponding to an angle of 300° in
standard position.
|
|
|
12.
|
Determine the point in quadrant II where the line represented by 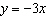 intersects
the unit circle. A | (0.95, –0.32) | C | (–0.35, 0.94) | B | (–0.32, 0.95) | D | (–0.32,
0.94) |
|
|
|
13.
|
The point P(0.391, 0.921) is the point of intersection of a unit circle and the
terminal arm of an angle q in standard position. What is the equation of
the line passing through the centre of the circle and the point P? Round the slope to two decimal
places.
|
|
|
14.
|
Which function, where x is in radians, is represented by the graph shown
below? 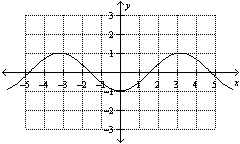
|
|
|
15.
|
Which graph represents the function y = 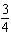 cos( 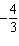 x x),
where x is in degrees?
|
|
|
16.
|
Determine the phase shift of the sinusoidal function 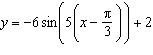 . A | 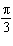 units to the right units to the right | C | 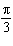 units to the
left units to the
left | B | 3p units to the left | D | 3p units to the
right |
|
|
|
17.
|
Solve 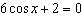 to three decimal places on the interval 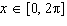 . A | x = 0.340, x = 5.943 | C | x = 1.911, x =
1.231 | B | x = 1.231, x = 5.052 | D | x = 1.911, x =
4.373 |
|
|
|
18.
|
Express 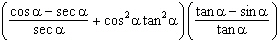 in terms of cosine and sine only, and simplify. A | 0 | C | 1 | B | 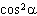 | D | 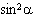 |
|
|
|
19.
|
Which expression is equivalent to 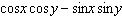 ?
|
|
|
20.
|
A bacteria colony initially has 1500 cells and doubles every week. Which
function can be used to model the population, p, of the colony after t days?
|
|
|
21.
|
An investment of $150 is placed into an account that earns interest, compounded
annually, at a rate of 5% for 12 years. The amount, A, in the account can be modelled by the
function 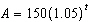 , where t is the time, in years. What is the domain of this function?
|
|
|
22.
|
Mohamed purchased a car for $16 000. It depreciates by 20% of its current value
every year. How much will the car be worth 8 years after it is purchased?
A | $80 000 | C | $2684.35 | B | $2000 | D | $68 797.07 |
|
|
|
23.
|
Evaluate 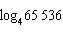 .
|
|
|
24.
|
Compared to the graph of the base function 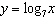 , the graph of the
function 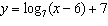 is translated A | 6 units to the right and 7 units up | C | 7 units to the right and 6 units
up | B | 7 units to the left and 6 units down | D | 6 units to the left and 7 units
down |
|
|
|
25.
|
Which function represents a vertical translation of 7 units down, a horizontal
translation of 8 units right, a horizontal stretch by a factor of 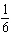 , no reflection in the
y-axis, a vertical stretch by a factor of 6, and no reflection in the x-axis, when compared to the
base function 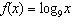 .
|
|
|
26.
|
The pH scale is used to measure the acidity or alkalinity of a solution. pH is
defined as 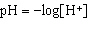 , where 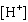 is the concentration of hydronium ions,
measured in moles per litre. Determine the pH of a solution with a concentration of 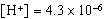 . Round your
answer to two decimal places.
|
|
|
27.
|
Solve 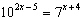 . Round your answer to two decimal places.
|
|
|
28.
|
What is the equation for the vertical asymptote of the graph of the function
shown? 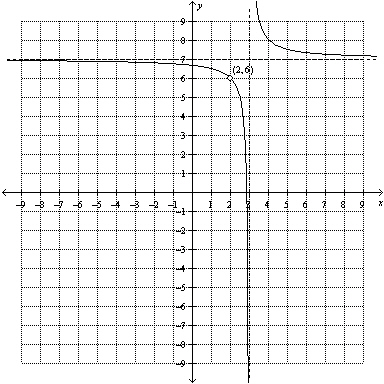
|
|
|
For the following question(s), assume that x is in radians, if
applicable.
|
|
|
29.
|
Given the functions 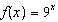 and 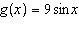 , what is the range of the composite
function 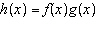 ?
|
|
|
30.
|
Given the functions 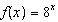 and 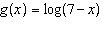 , determine the domain of the combined
function 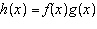 .
|
|
|
31.
|
If 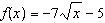 and 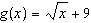 , what are the restrictions on the domain
for the combined function 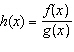 ?
|
|
|
32.
|
The number of different ways that 9 bikes can be locked in a bike rack is
A | 3 628 800 | C | 40 320 | B | 20 160 | D | 362 880 |
|
|
|
33.
|
Evaluate 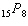 . A | 32 432 400 | C | 6435 | B | 163 459 296 000 | D | 259 459 200 |
|
|
|
34.
|
Determine the 5th term in the expansion of 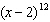 .
|
|
|
35.
|
While at the dollar store, Peter finds 19 items at $1 each that he wants, but he
only has $3. The number of ways he could select which items to buy is
|
Short Answer
|
|
|
1.
|
Solve the equation 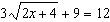 , 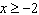 , algebraically.
|
|
|
2.
|
Find the exact value of 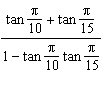 .
|
|
|
3.
|
|
|
|
4.
|
Given 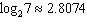 , find the value of 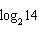 .
|
|
|
For the following question(s), assume that x is in radians, if
applicable.
|
|
|
5.
|
Determine the domain and range of the function 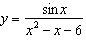 .
|
Problem
|
|
|
1.
|
Prove that x2 + 5x + 6 is a factor of
x4 + 5x3 + 2x2 – 20x –
24.
|
|
|
2.
|
a) Without using a calculator, determine two angles between 0° and
360° that have a sine ratio of 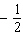 . b) Use a calculator and a diagram to verify
your answers to part a).
|
|
|
3.
|
Determine the number of solutions for the trigonometric equation 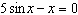 on the
interval 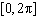 .
|
|
|
4.
|
A cosine function has half the period of the function 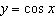 . All other
properties of the two functions are identical. a) Determine the number of points of
intersection if these two functions are graphed on the interval 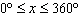 . Explain. b)
Determine the values of x of the first two points of intersection to the right of x =
0°. c) If the graph of the two functions were extended to 720°, how many points
of intersection would there be? Explain. d) Use the concept of coterminal angles to
determine the values of x where the points of intersection would occur. e) Graph the
two functions over the interval 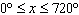 to verify your answer for parts b), c), and d).
|
|
|
5.
|
Prove that the equation 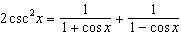 is true for all values of
x.
|