Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Compared to the graph of the base function 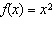 , the graph of the
function 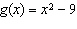 is translated A | 9 units to the left | C | 9 units down | B | 9 units to the right | D | 9 units up |
|
|
|
2.
|
The function 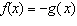 represents a transformation that can best be described as
A | a reflection in the x-axis | C | a reflection in the
y-axis | B | a reflection in the x-axis and the y-axis | D | a reflection in the line y =
x |
|
|
|
3.
|
What are the coordinates of the invariant point(s) when the function 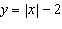 is
reflected in the y-axis? A | (2, –2) | C | (0, –2) | B | (–2, 0) and (2, 0) | D | (0, 2) |
|
|
|
4.
|
When the value of a is less than –1, the function 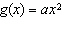
has what relationship to the base function 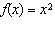 ? A | f(x) is compressed vertically | B | f(x) is
reflected and compressed vertically | C | f(x) is stretched
vertically | D | f(x) is reflected and stretched
vertically |
|
|
|
5.
|
Compared to the graph of the base function 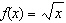 , the graph of the
function 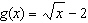 is translated A | 2 units up | C | 2 units to the left | B | 2 units to the right | D | 2 units down |
|
|
|
6.
|
Compared to the graph of the base function 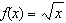 , the graph of the
function 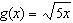 is A | compressed by a factor of 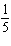 and not reflected and not reflected | B | stretched by a factor
of 5 and reflected in the y-axis | C | compressed by a factor of 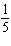 and reflected
in the y-axis and reflected
in the y-axis | D | stretched by a factor of 5 and not reflected |
|
|
|
7.
|
What is the equation of the radical function shown in the graph below? 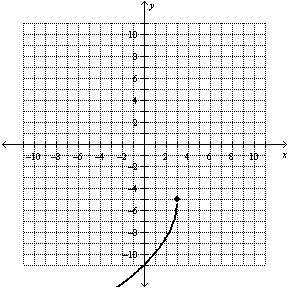
|
|
|
8.
|
Which graph shows the solution to the radical equation 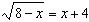 ?
|
|
|
9.
|
Which graph shows the solution to the radical equation 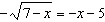 ?
|
|
|
10.
|
What is the remainder when 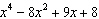 is divided by 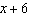 ?
|
|
|
11.
|
If 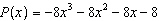 is divided by 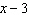 , what is the
remainder?
|
|
|
12.
|
A factor of 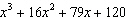 is A | 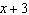 | C | 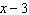 | B | x –
5 | D | x –
8 |
|
|
|
13.
|
Given the function 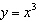 , what are the parameters of the transformed function
y = 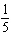 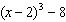 and what is the effect of each parameter on the graph of
the original function? A | a = 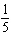 , vertical stretch about the x-axis by a factor of , vertical stretch about the x-axis by a factor of
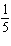
h = –8, horizontal translation 8 units right
k = 2, vertical
translation 2 units down | B | a =  , vertical stretch about
the x-axis by a factor of , vertical stretch about
the x-axis by a factor of 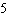
h = 2, horizontal translation 2 units
left
k = –8, vertical translation 8 units right | C | a = 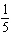 ,
vertical stretch about the x-axis by a factor of ,
vertical stretch about the x-axis by a factor of 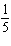
h = 2, horizontal translation 2
units right
k = –8, vertical translation 8 units down | D | a = 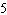 ,
vertical stretch about the x-axis by a factor of ,
vertical stretch about the x-axis by a factor of 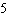
h = 2, horizontal translation
2 units right
k = –8, vertical translation 8 units
down |
|
|
|
14.
|
Determine the arc length of a circle with radius 5.5 cm if it is subtended by a
central angle of 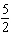 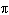 radians. Round your answer to one
decimal place. A | 1.4 cm | C | 4.4 cm | B | 43.2 cm | D | 6.9 cm |
|
|
|
15.
|
A ball is riding the waves at a beach. The ball’s up and down motion with
the waves can be described using the formula 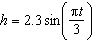 , where h is the height, in metres,
above the flat surface of the water and t is the time, in seconds. What is the height of the
ball, to the nearest hundredth of a metre, after t = 17 s? A | –0.87 m | C | –1.99 m | B | –2.66 m | D | 1.99 m |
|
|
|
16.
|
Which function is represented by the graph shown below, where q is in radians?
|
|
|
17.
|
Given the trigonometric function 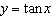 , find the value of the
y-coordinate of the point with x-coordinate –1200°.
|
|
|
Use the following information to answer the questions.The height,
h, in centimetres, of a piston moving up and down in an engine cylinder can be modelled by the
function 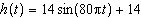 , where t is the time, in seconds.
|
|
|
18.
|
What is the piston’s minimum height?
|
|
|
19.
|
Which equation is a Pythagorean identity?
|
|
|
20.
|
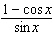 can be rewritten as
|
|
|
21.
|
What is the solution to the equation 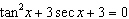 over the domain 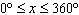 ? A | 60° and 240° | C | no solution | B | 120°, 180°, and 240° | D | 120° |
|
|
|
22.
|
The domain of the function 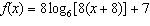 is
|
|
|
23.
|
Compared to the graph of the base function 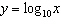 , the graph of the
function 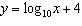 is translated A | 4 units to the left | C | 4 units up | B | 4 units down | D | 4 units to the
right |
|
|
|
24.
|
Compared to the graph of the base function 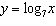 , the graph of the function
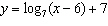 is translated A | 6 units to the right and 7 units up | C | 7 units to the right and 6 units
up | B | 7 units to the left and 6 units down | D | 6 units to the left and 7 units
down |
|
|
|
25.
|
Compared to the graph of the base function 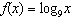 , the graph of the
function 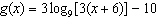 is A | translated down 10 units and left 6 units, horizontally stretched by a factor of 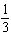 ,
reflected in the y-axis, vertically stretched by a factor of 3, and reflected in the
x-axis ,
reflected in the y-axis, vertically stretched by a factor of 3, and reflected in the
x-axis | C | translated down 10 units and left 6 units, horizontally stretched by a factor of 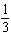 ,
not reflected in the y-axis, vertically stretched by a factor of 3, and not reflected in the
x-axis ,
not reflected in the y-axis, vertically stretched by a factor of 3, and not reflected in the
x-axis | B | translated down 10 units and right 6 units, horizontally stretched by a factor of
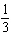 , reflected in the y-axis, vertically stretched by a factor of 3, and not reflected in the
x-axis , reflected in the y-axis, vertically stretched by a factor of 3, and not reflected in the
x-axis | D | translated up 10
units and left 6 units, horizontally stretched by a factor of 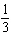 , not reflected in the
y-axis, vertically stretched by a factor of 3, and not reflected in the
x-axis , not reflected in the
y-axis, vertically stretched by a factor of 3, and not reflected in the
x-axis |
|
|
|
26.
|
Which graph represents the function 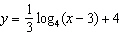 ?
|
|
|
27.
|
Solve the equation 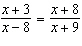 . A | x = –3 | C | x = 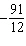 | B | x = 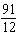 | D | x = 8,
x = –9 |
|
|
|
28.
|
Solve the equation 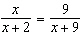 . A | 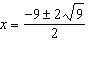 | C | no solution | B | x = 2,
x = 9 | D | 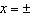 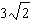 |
|
|
|
29.
|
Given the functions 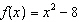 and 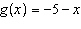 , determine an equation for the combined
function 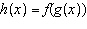 .
|
|
|
30.
|
If 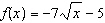 and 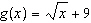 , what are the restrictions on the domain
for the combined function 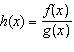 ?
|
|
|
31.
|
Evaluate 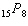 . A | 32 432 400 | C | 6435 | B | 163 459 296 000 | D | 259 459 200 |
|
|
|
32.
|
An orchestra has 2 violinists, 3 cellists, and 4 harpists. Assume that the
players of each instrument have to sit together, but they can sit in any position in their own group.
In how many ways can the conductor seat the members of the orchestra in a line?
|
|
|
33.
|
For which of the following terms is a = 55 in the expansion of (x
+ y)11?
|
|
|
34.
|
A scout troop is arranged in a circle for an opening ceremony. If there are 9
scouts, in how many unique ways can they stand around the circle?
|
|
|
35.
|
Suppose that 10 non-collinear points are plotted on a plane. Which expression
represents the number of triangles that can be formed using these points?
|
Short Answer
|
|
|
1.
|
a) Sketch the graph of 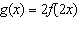 for each base function. i) 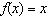 ii) ii) 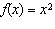 iii) iii) 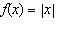 b) b) Write the equation for
g( x) to represent a single stretch that results in the same graph as in each function
in part a). c) Describe how each stretch affects the domain and range for each
function.
|
|
|
2.
|
a) Sketch the graph of each function 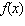 , and then sketch the graph
of 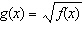 . i) 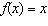 ii) ii) 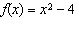 iii) iii) 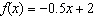 b) b)
State the domain and range of each f( x) and g( x).
|
|
|
3.
|
Factor fully.
a) x3 + 6x2 +
11x + 6
b) 4x3 – 11x2 –
3x
c) x4 – 81
|
|
|
4.
|
Find the exact value of 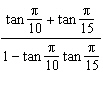 .
|
|
|
5.
|
Consider the function 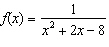 . a) Determine the key features
of the function: i) domain and
range ii) intercepts
iii) equations of any asymptotes b) Sketch the graph of the function. 
|
Problem
|
|
|
1.
|
Two skydivers jump out of a plane. The first skydiver’s motion can be
modelled by the function 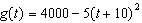 . The second skydiver jumps 10 s later with a goal of
catching up to the first skydiver. The motion of the second skydiver can be modelled by 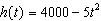 .
For both functions, the height is measured in metres and the time is the number of seconds after the
second skydiver jumps. a) Graph the functions on the same set of axes. b) Will
the second skydiver catch up to the first before they have to open their parachutes at 800
m? c) State the domain and range of these functions in this context.
|
|
|
2.
|
Sketch the graphs of 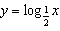 , 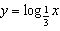 , and 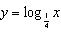 , and then
describe the pattern in terms of n for 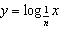 .
|
|
|
3.
|
Prove that 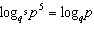 .
|
|
|
4.
|
A vehicle depreciates 20% in value in the first year and 10% in each year after
the first. a) Write a function, 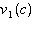 , to describe the value of the vehicle
after 1 year in terms of the original cost, c. b) Write a function, 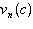 , to describe
the value after n years in terms of the original cost, c. c) If the original
value of the vehicle is $45 000, what is its value after 5 years?
|
|
|
5.
|
The chorus of a play has 17 females and 13 males. The director wishes to meet
with 6 of them to discuss the upcoming production.
a) How many selections are
possible?
b) How many selections are possible if the group consists of three females and
three males?
c) One of the male students is named Ajay. How many six-member selections
consisting of Ajay, two other males, and three females are possible?
|