Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Compared to the graph of the base function 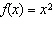 , the graph of the
function 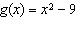 is translated A | 9 units to the left | C | 9 units down | B | 9 units to the right | D | 9 units up |
|
|
|
2.
|
What is the equation of the transformed function, g( x), after the
transformations are applied to the graph of the base function 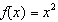 , shown in blue, to
obtain the graph of g( x), shown in red? 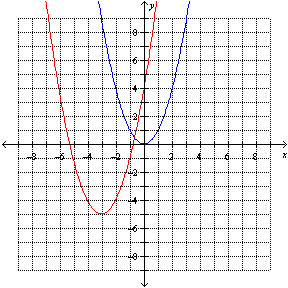
|
|
|
3.
|
The function 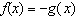 represents a transformation that can best be described as
A | a reflection in the x-axis | C | a reflection in the
y-axis | B | a reflection in the x-axis and the y-axis | D | a reflection in the line y =
x |
|
|
|
4.
|
When a function is reflected in the x-axis, the coordinates of point
(x, y) become
A | (x, –y) | C | (–x, –y) | B | (–x,
y) | D | (x,
y) |
|
|
|
5.
|
When a > 0, the function 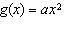 has what relationship to the base
function 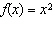 ? A | f(x) is stretched vertically by a factor of |a| and reflected in the
x-axis | B | f(x) is stretched horizontally by a factor of 1/|a| | C | f(x) is
stretched vertically by a factor of |a| | D | f(x) is stretched horizontally by
a factor of 1/|a| and reflected in the y-axis |
|
|
|
6.
|
Which of the graphs shown below represents the base function 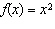 and the
stretched function g( x) = 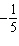 x2 x2?
|
|
|
7.
|
Compared to the graph of the base function 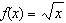 , the graph of the
function 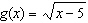 is translated A | 5 units down | C | 5 units right | B | 5 units left | D | 5 units up |
|
|
|
8.
|
Which point on the graph 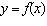 does not exist on the graph of 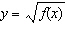 ?
|
|
|
9.
|
Which graph represents an even-degree polynomial function with a
y-intercept of 9?
|
|
|
10.
|
What is the remainder when 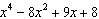 is divided by 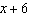 ?
|
|
|
11.
|
What is the maximum number of real distinct roots that a cubic equation can
have?
|
|
|
12.
|
Given the function 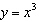 , what are the parameters of the transformed function
y = 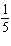 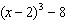 and what is the effect of each parameter on the graph of
the original function? A | a = 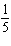 , vertical stretch about the x-axis by a factor of , vertical stretch about the x-axis by a factor of
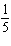
h = –8, horizontal translation 8 units right
k = 2, vertical
translation 2 units down | B | a = 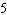 , vertical stretch about
the x-axis by a factor of , vertical stretch about
the x-axis by a factor of 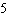
h = 2, horizontal translation 2 units
left
k = –8, vertical translation 8 units right | C | a = 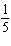 ,
vertical stretch about the x-axis by a factor of ,
vertical stretch about the x-axis by a factor of 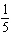
h = 2, horizontal translation 2
units right
k = –8, vertical translation 8 units down | D | a = 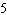 ,
vertical stretch about the x-axis by a factor of ,
vertical stretch about the x-axis by a factor of 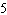
h = 2, horizontal translation
2 units right
k = –8, vertical translation 8 units
down |
|
|
|
13.
|
Which point on the unit circle corresponds to tan
q = 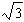 ? ?
|
|
|
14.
|
The point P(0.391, 0.921) is the point of intersection of a unit circle and the
terminal arm of an angle q in standard position. What is the equation of
the line passing through the centre of the circle and the point P? Round the slope to two decimal
places.
|
|
|
15.
|
Giai got an answer of 3.86 when she was calculating the value of a trigonometric
function. Assuming Giai did her calculation correctly, which of the following was she
calculating?
|
|
|
16.
|
Which graph represents the function y = 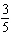 sin (  q) q), where q is in radians?
|
|
|
17.
|
What is the period of the sinusoidal function 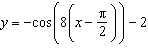 ?
|
|
|
18.
|
Which graph represents the sinusoidal function 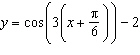 ?
|
|
|
19.
|
Give an equation for a transformed sine function with an amplitude of 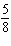 , a
period of 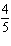 , a phase shift of 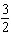 rad to the right, and a vertical translation of 9 units
down.
|
|
|
20.
|
What does the expression 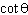 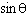 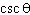 simplify to?
|
|
|
21.
|
Determine the exact value of 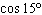 .
|
|
|
22.
|
Simplify 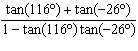 .
|
|
|
23.
|
Which expression is equivalent to 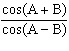 ?
|
|
|
24.
|
What is the general solution, in radians, to the equation 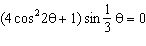 ? A | 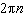 where where 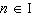 | C | 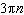 where where 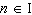 | B | no solution | D | 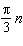 where where 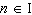 |
|
|
|
25.
|
Mohamed purchased a car for $16 000. It depreciates by 20% of its current value
every year. How much will the car be worth 8 years after it is purchased?
A | $80 000 | C | $2684.35 | B | $2000 | D | $68 797.07 |
|
|
|
26.
|
Compared to the graph of the base function 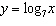 , the graph of the function
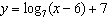 is translated A | 6 units to the right and 7 units up | C | 7 units to the right and 6 units
up | B | 7 units to the left and 6 units down | D | 6 units to the left and 7 units
down |
|
|
|
27.
|
Which graph represents the function 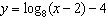 ?
|
|
|
28.
|
Which graph represents the function 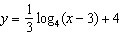 ?
|
|
|
29.
|
What is the equation for the horizontal asymptote of the graph of the function
shown? 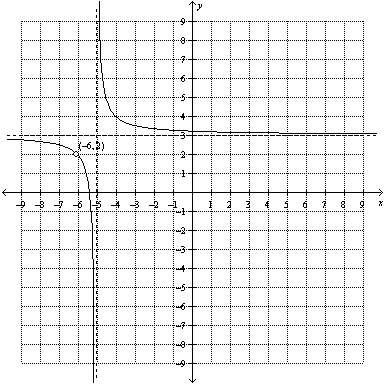
|
|
|
30.
|
Given the functions 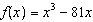 and 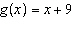 , determine the simplified equation for
the combined function 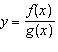 .
|
|
|
For the following question(s), assume that x is in radians, if
applicable.
|
|
|
31.
|
Given the functions 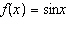 and 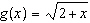 , what is the value of 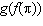 ?
|
|
|
32.
|
Given the function 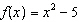 , determine the value of 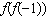 .
|
|
|
33.
|
Solve for the variable: 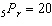 A | 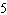 | C | 60 | B | 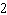 | D | 7 |
|
|
|
34.
|
Jenni and Hari go to a local Chinese restaurant for dim sum. If there are 20
items on the menu, and Jenni orders 7 items and Hari orders 11 items, which expression represents the
total number of choices between them?
|
|
|
35.
|
While at the dollar store, Peter finds 19 items at $1 each that he wants, but he
only has $3. The number of ways he could select which items to buy is
|
Short Answer
|
|
|
1.
|
Determine the value of 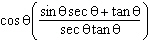 if 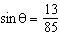 and 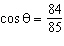 .
|
|
|
2.
|
If 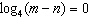 and 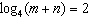 , determine the values of m and
n.
|
|
|
3.
|
A certain type of exponential growth can be described by the equation 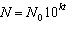 ,
where 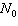 is the initial amount; k is the doubling time, in years; and N is the
amount after time, t, in years, has passed. Suppose that the population of a small town
doubles every 25 years. How long does it take to triple, to the nearest tenth of a year?
|
|
|
4.
|
Consider the function 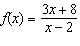 . a) Determine the key features
of the function: i) domain and
range ii) intercepts
iii) equations of any asymptotes b) Sketch the graph of the function. 
|
|
|
5.
|
Josie goes to the local submarine sandwich shop. She can choose from 21 types of
sandwiches. There are 3 types of cheese, 8 types of vegetables, and 7 types of sauce. Assuming that
Josie only chooses one type of cheese, one vegetable, and one sauce for her sandwich, how many
choices does she have?
|
Problem
|
|
|
1.
|
The graph of 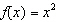 is transformed to the graph of 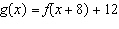 . a) Describe the
two translations represented by this transformation. b) Determine three points on the base
function. Horizontally translate and then vertically translate the points. What are the three
resulting image points?
|
|
|
2.
|
The air quality index, I, in a large city can be modelled by the equation
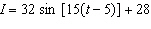 , where t represents the time, in hours, after midnight. New legislation has been
introduced that is expected to decrease the pollution levels in the city so that the index values
will decrease to 90% of current values in 10 years. a) What are the current minimum and
maximum values of the index in the city? b) At what time of the day is the air quality
index at a maximum? c) If an air quality alert is issued for times when the index is above
48, during what time period will an air quality alert be issued? d) What factors in the
equation for air quality index will be affected by the legislation? Explain how they will be
affected. e) What will the new air quality index equation be based on your answers in part
d)? f) How will these changes affect the times when an air quality alert will be
issued?
|
|
|
3.
|
An angle satisfies the relation 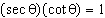 . a) Use the definition of the
reciprocal trigonometric ratios to express the left side of the relation in terms of the sine and/or
cosine ratios. b) Determine the value(s) for the angle. Do not use a
calculator. c) Verify your answer to part b) using a calculator. d) Show your
answer to part b) using a unit circle.
|
|
|
4.
|
Sketch the graphs of 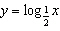 , 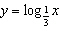 , and 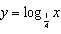 , and then
describe the pattern in terms of n for 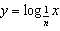 .
|
|
|
5.
|
A photographer uses a light meter to measure the intensity of light from a flash
bulb. The intensity, I, in lux, of the flash bulb is a function of the distance, d, in
metres, from the light and can be represented by 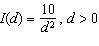 . a) Determine the following,
to two decimal places: i) the intensity of light 3 m from
the flash bulb ii) the average rate of change in the
intensity of light for the interval 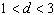 b) b) What does the sign of your answer to part
a)ii) indicate about the light intensity?
|