Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Given the graph of f( x) shown below, what are the coordinates of
point A if the transformed graph is represented by 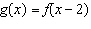 ? 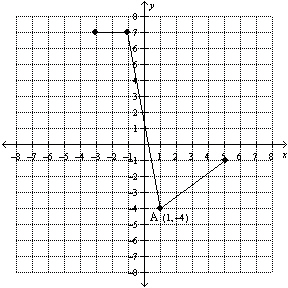
|
|
|
2.
|
When b > 0, the function 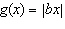 has what relationship to the base
function 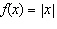 ? A | f(x) is stretched vertically by a factor of |b| and reflected in the
x-axis | B | f(x) is stretched vertically by a factor of |b| | C | f(x) is
stretched horizontally by a factor of 1/|b| and reflected in the y-axis | D | f(x) is
stretched horizontally by a factor of 1/|b| |
|
|
|
3.
|
Which of the graphs shown below represents the base function 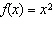 and the
stretched function g( x) = ( 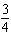 x x) 2?
|
|
|
4.
|
Compared to the graph of the base function 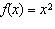 , the graph of the function
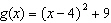 is translated A | 9 units to the left and 4 units down | C | 9 units to the right and 4 units
up | B | 4 units to the left and 9 units down | D | 4 units to the right and 9 units
up |
|
|
|
5.
|
What is the equation of the transformed function, g( x), after the
transformations are applied to the graph of the base function 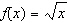 , shown in blue, to
obtain the graph of g( x), shown in red? 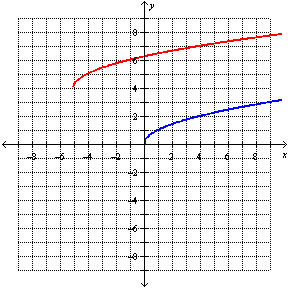
|
|
|
6.
|
Which graph represents an odd-degree polynomial function with two
x-intercepts?
|
|
|
7.
|
How many x-intercepts are possible for the polynomial function 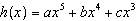 ?
|
|
|
8.
|
If 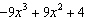 is divided by 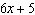 , then the restriction on x
is
|
|
|
9.
|
If 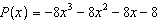 is divided by 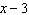 , what is the
remainder?
|
|
|
10.
|
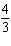 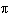 radians is equal to how many degrees?
|
|
|
11.
|
Which of the following angles, in degrees, is coterminal with, but not equal to,
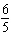 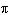 radians?
|
|
|
12.
|
Determine the arc length of a circle with radius 5.5 cm if it is subtended by a
central angle of 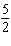 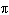 radians. Round your answer to one
decimal place. A | 1.4 cm | C | 4.4 cm | B | 43.2 cm | D | 6.9 cm |
|
|
|
13.
|
If the angle q is –5000° in standard
position, it can be described as having made
A | 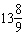 rotations rotations | C | 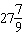 rotations
rotations | B | 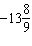 rotations rotations | D | 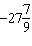 rotations rotations |
|
|
|
14.
|
A ball is riding the waves at a beach. The ball’s up and down motion with
the waves can be described using the formula 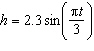 , where h is the height, in metres,
above the flat surface of the water and t is the time, in seconds. What is the height of the
ball, to the nearest hundredth of a metre, after t = 17 s? A | –0.87 m | C | –1.99 m | B | –2.66 m | D | 1.99 m |
|
|
|
15.
|
A tricycle has a front wheel that is 30 cm in diameter and two rear wheels that
are each 12 cm in diameter. If the front wheel rotates through a angle of 32°, through how many
degrees does each rear wheel rotate, to the nearest tenth of a degree?
A | 32.0° | C | 80.0Á | B | 40.0Á | D | 160.0Á |
|
|
|
16.
|
Which function is represented by the graph shown below, where q is in radians?
|
|
|
17.
|
Determine the phase shift of the sinusoidal function 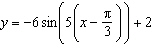 . A | 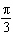 units to the right units to the right | C | 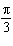 units to the
left units to the
left | B | 3p units to the left | D | 3p units to the
right |
|
|
|
18.
|
Which graph represents the sinusoidal function 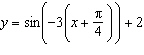 ?
|
|
|
19.
|
Give an equation for a transformed sine function with an amplitude of 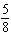 , a
period of 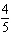 , a phase shift of 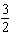 rad to the right, and a vertical translation of 9 units
down.
|
|
|
Use the following information to answer the questions.The height,
h, in centimetres, of a piston moving up and down in an engine cylinder can be modelled by the
function 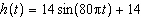 , where t is the time, in seconds.
|
|
|
20.
|
What is the period?
|
|
|
21.
|
What does the expression 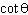 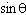 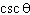 simplify to?
|
|
|
22.
|
Which expression is equivalent to 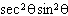 ?
|
|
|
23.
|
What is the general solution, in degress, to the equation 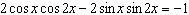 ?
|
|
|
24.
|
Which graph represents the function 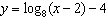 ?
|
|
|
25.
|
The pH scale is used to measure the acidity or alkalinity of a solution. pH is
defined as 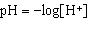 , where 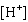 is the concentration of hydronium ions, measured in moles
per litre. Determine the pH of a solution with a concentration of 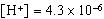 . Round your answer to two
decimal places.
|
|
|
26.
|
What is the value of k in the function 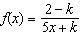 if its graph passes
through the point (3, 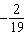 ) ? A | 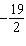 | C | –10 | B | 4 | D | No such k
exists |
|
|
|
27.
|
Given the functions 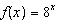 and 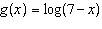 , determine the domain of the combined
function 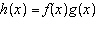 .
|
|
|
28.
|
If 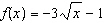 and 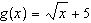 , what is the simplified combined function
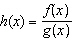 ?
|
|
|
29.
|
What is the value of 6!?
|
|
|
30.
|
Solve for the variable: 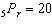 A | 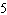 | C | 60 | B | 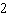 | D | 7 |
|
|
|
31.
|
Evaluate the expression 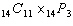 . A | 2184 | C | 794 976 | B | 87 178 291 200 | D | 239 500 800 |
|
|
|
32.
|
After the tryouts for the volleyball team, the coach selects 14 people to join
the team. Due to a problem with transportation, only 9 people can travel. In how many ways can the
coach pick the people to go?
A | 726 485 760 | C | 630 | B | 2002 | D | 126 |
|
|
|
33.
|
For a mock United Nations, 6 boys and 7 girls are to be chosen. If there are 12
boys and 9 girls to choose from, how many groups are possible?
A | 846 720 | C | 960 | B | 33 264 | D | 120 708 403 200 |
|
|
|
34.
|
A scout troop is arranged in a circle for an opening ceremony. If there are 9
scouts, in how many unique ways can they stand around the circle?
|
|
|
35.
|
The leadership committee at a high school has 4 grade 10 students, 2 grade 11
students, and 6 grade 12 students. This year, 12 grade 10, 8 grade 11, and 10 grade 12 students
applied for the committee. How many ways are there to select the committee?
A | 2 910 600 | C | 733 | B | 100 590 336 000 | D | 163 136 |
|
Short Answer
|
|
|
1.
|
For each of the following, describe the combination of transformations that must
be applied to the graph of 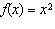 (shown in blue) to obtain the graph of g( x)
(shown in red). a) 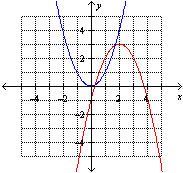 b) b) 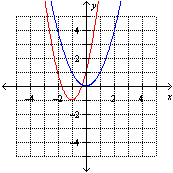 c) c) 
|
|
|
2.
|
|
|
|
3.
|
Factor fully.
a) x3 + 6x2 +
11x + 6
b) 4x3 – 11x2 –
3x
c) x4 – 81
|
|
|
4.
|
A child swings on a playground swing set. If the length of the swing’s
chain is 3 m and the child swings through an angle of 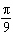 , what is the exact arc length through
which the child travels?
|
|
|
5.
|
A population, p, of bears varies according to 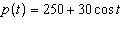 , where
t is the time, in years, and angles are measured in radians. a) What are the maximum
and minimum populations? b) What is the first interval, in years and months, over which the
population is increasing?
|
Problem
|
|
|
1.
|
Two skydivers jump out of a plane. The first skydiver’s motion can be
modelled by the function 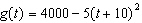 . The second skydiver jumps 10 s later with a goal of
catching up to the first skydiver. The motion of the second skydiver can be modelled by 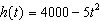 .
For both functions, the height is measured in metres and the time is the number of seconds after the
second skydiver jumps. a) Graph the functions on the same set of axes. b) Will
the second skydiver catch up to the first before they have to open their parachutes at 800
m? c) State the domain and range of these functions in this context.
|
|
|
2.
|
An initial investment of $4000 earns interest at 4% per year, compounded
annually.
a) Create a table of values for the first 10 years of the investment. Round the
amounts to the nearest cent.
b) Graph the data from your table of values.
c) Is
the relationship between the time and the amount of the investment exponential? Explain.
d)
Write an equation to represent the data.
|
|
|
3.
|
a) Write an equation to represent a rational function with the following
conditions: • reciprocal of a quadratic function • asymptotes with equations 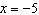 ,
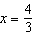 , and 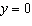 • 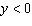 whenever 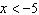 or 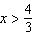 b) b)
How many such equations are there? Explain your answer.
|
|
|
4.
|
A vehicle depreciates 20% in value in the first year and 10% in each year after
the first. a) Write a function, 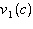 , to describe the value of the vehicle
after 1 year in terms of the original cost, c. b) Write a function, 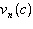 , to describe
the value after n years in terms of the original cost, c. c) If the original
value of the vehicle is $45 000, what is its value after 5 years?
|
|
|
5.
|
To win the grand prize in lottery A, a player must select all six of the winning
numbers drawn from the numbers 1 to 49. To win in lottery B, a player must select all seven of the
winning numbers drawn from 1 to 49. Bernadette argues that the chances of randomly selecting the
winning number for lottery A are seven times as good as winning for lottery B. Create an argument to
agree or disagree with this statement.
|