Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
When a function is reflected in the x-axis, the coordinates of point
(x, y) become
A | (x, –y) | C | (–x, –y) | B | (–x,
y) | D | (x,
y) |
|
|
|
2.
|
What are the coordinates of the invariant point(s) when the function 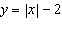 is
reflected in the y-axis? A | (2, –2) | C | (0, –2) | B | (–2, 0) and (2, 0) | D | (0, 2) |
|
|
|
3.
|
Compared to the graph of the base function 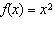 , the graph of the function
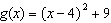 is translated A | 9 units to the left and 4 units down | C | 9 units to the right and 4 units
up | B | 4 units to the left and 9 units down | D | 4 units to the right and 9 units
up |
|
|
|
4.
|
Compared to the graph of the base function 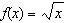 , the graph of the
function 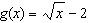 is translated A | 2 units up | C | 2 units to the left | B | 2 units to the right | D | 2 units down |
|
|
|
5.
|
Compared to the graph of the base function 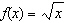 , the graph of the
function 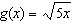 is A | compressed by a factor of 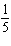 and not reflected and not reflected | B | stretched by a factor
of 5 and reflected in the y-axis | C | compressed by a factor of 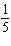 and reflected
in the y-axis and reflected
in the y-axis | D | stretched by a factor of 5 and not reflected |
|
|
|
6.
|
Which equation of a radical function would have the following domain and
range? 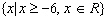 ; 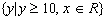
|
|
|
7.
|
If 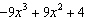 is divided by 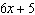 , then the restriction on x
is
|
|
|
8.
|
Determine the value of k so that 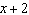 is a factor of 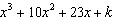 . A | k = –1 | C | k = 14 | B | k = –14 | D | k = 1 |
|
|
|
9.
|
One root of the equation 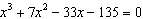 is
|
|
|
10.
|
Which of the following angles, in degrees, is coterminal with, but not equal to,
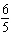 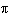 radians?
|
|
|
11.
|
Determine the equation of a circle with centre at the origin and radius
8.
|
|
|
12.
|
A ball is riding the waves at a beach. The ball’s up and down motion with
the waves can be described using the formula 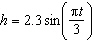 , where h is the height, in metres,
above the flat surface of the water and t is the time, in seconds. What is the height of the
ball, to the nearest hundredth of a metre, after t = 17 s? A | –0.87 m | C | –1.99 m | B | –2.66 m | D | 1.99 m |
|
|
|
13.
|
Determine the point in quadrant II where the line represented by 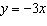 intersects the
unit circle. A | (0.95, –0.32) | C | (–0.35, 0.94) | B | (–0.32, 0.95) | D | (–0.32,
0.94) |
|
|
|
14.
|
Which graph represents the sinusoidal function 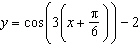 ?
|
|
|
15.
|
Solve 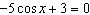 , to the nearest tenth of a degree, if necessary, on the
interval 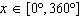 . A | x = 53.1°, x = 126.9° | C | x = 36.9°, x =
323.1° | B | x = 126.9°, x = 233.1° | D | x = 53.1°, x = 306.9° |
|
|
|
16.
|
Which equation is a reciprocal identity?
|
|
|
17.
|
Which expression is equivalent to 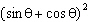 ?
|
|
|
18.
|
Determine the exact value of 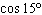 .
|
|
|
19.
|
Which expression is equivalent to 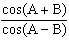 ?
|
|
|
20.
|
What is the general solution, in radians, to the equation 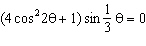 ? A | 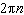 where where 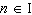 | C | 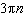 where where 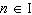 | B | no solution | D | 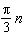 where where 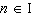 |
|
|
|
21.
|
An investment of $150 is placed into an account that earns interest, compounded
annually, at a rate of 5% for 12 years. The amount, A, in the account can be modelled by the
function 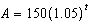 , where t is the time, in years. What is the domain of this function?
|
|
|
22.
|
Jennifer deposited some money into an account that pays 7% per year, compounded
annually. Today her balance is $300. How much was in the account 10 years ago, to the nearest
cent? [Hint: Use 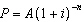 .] A | $163.18 | C | $42.86 | B | $30.00 | D | $152.50 |
|
|
|
23.
|
Which graph represents the function 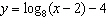 ?
|
|
|
24.
|
Which graph represents the function 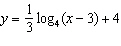 ?
|
|
|
25.
|
What is the equation for the horizontal asymptote of the graph of the function
shown? 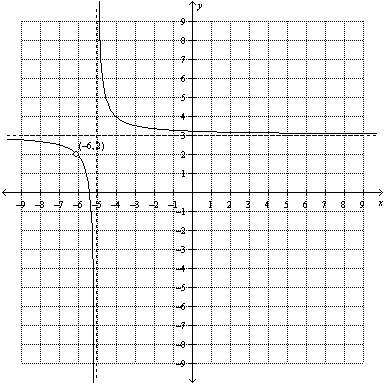
|
|
|
26.
|
Solve the equation 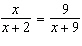 . A | 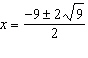 | C | no solution | B | x = 2,
x = 9 | D | 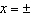 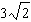 |
|
|
|
27.
|
Given the functions 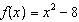 and 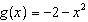 , determine the equation for the combined
function 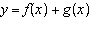 .
|
|
|
For the following question(s), assume that x is in radians, if
applicable.
|
|
|
28.
|
Shown is the graph of 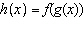 , where 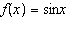 and 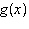 is a function
of the form 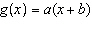 .
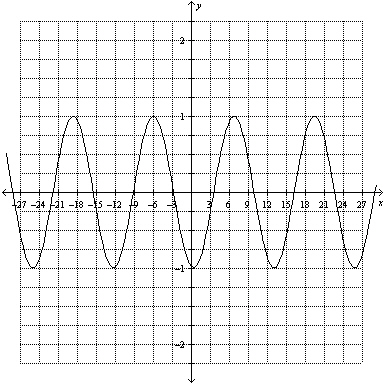
What
equation represents 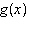 ?
|
|
|
29.
|
Given the functions 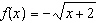 and 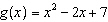 , what is the domain of the combined
function 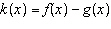 ?
|
|
|
30.
|
Given the functions 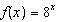 and 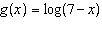 , determine the domain of the combined
function 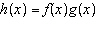 .
|
|
|
31.
|
Given the functions 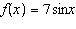 and 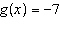 , determine the range of the combined
function 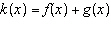 .
|
|
|
32.
|
What is the value of 6!?
|
|
|
33.
|
Solve for n in the expression 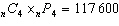 .
|
|
|
34.
|
After the tryouts for the volleyball team, the coach selects 14 people to join
the team. Due to a problem with transportation, only 9 people can travel. In how many ways can the
coach pick the people to go?
A | 726 485 760 | C | 630 | B | 2002 | D | 126 |
|
|
|
35.
|
Rachael has a digital music player that holds 800 songs. She has 1500 songs in
her music library. She decides that her 50 favourite songs must be on the player. Which expression
can be used to calculate the number of ways can she load songs on to the MP3 player so that it is
full?
|
Short Answer
|
|
|
1.
|
a) Use long division to divide x3 +
3x2 – 7 by x + 2. Express the result in quotient form.
b)
Identify any restrictions on the variable.
c) Write the corresponding statement that can be
used to check the division.
d) Verify your answer.
|
|
|
2.
|
Find the exact value of 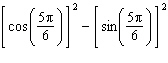 . .
|
|
|
3.
|
Joe wants to travel from his home to school. The school is 6 blocks east and 6
blocks north. How many routes can Joe take from his house to school if he only moves east and
north. 
|
|
|
4.
|
Simplify the expression 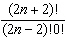 .
|
|
|
5.
|
A neon sign with the words “Espresso Coffee” on it has 5 letters
burnt out. In how many ways can you select 3 good letters and 2 burnt-out letters?
|
Problem
|
|
|
1.
|
Two skydivers jump out of a plane. The first skydiver’s motion can be
modelled by the function 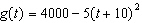 . The second skydiver jumps 10 s later with a goal of
catching up to the first skydiver. The motion of the second skydiver can be modelled by 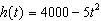 .
For both functions, the height is measured in metres and the time is the number of seconds after the
second skydiver jumps. a) Graph the functions on the same set of axes. b) Will
the second skydiver catch up to the first before they have to open their parachutes at 800
m? c) State the domain and range of these functions in this context.
|
|
|
2.
|
Sketch the graph of 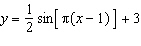 for two cycles, where angles are in
radians.
|
|
|
3.
|
The table shows the fraction of the Moon that can be seen at midnight from
Simone’s town. Day 1 represents January 1. Day | 1 | 2 | 3 | 4 | 5 | 6 | 10 | 14 | 19 | 21 | Fraction
Visible | 0.25 | 0.17 | 0.12 | 0.06 | 0.02 | 0.00 | 0.10 | 0.56 | 0.98 | 1.00 | | | | | | | | | | | |
| Day | 24 | 30 | 35 | 41 | 45 | 51 | 56 | 60 | 65 | 66 | Fraction
Visible | 0.78 | 0.33 | 0.02 | 0.15 | 0.65 | 1.00 | 0.78 | 0.30 | 0.01 | 0.00 | | | | | | | | | | | |
a) What is the period of the sine function that could be used to
model the data? b) What is the amplitude of the function? c) What is the phase
shift of the function? d) What is the vertical shift? e) Use your answers to
parts a) to d) to write an equation for the function. f) Use your function to determine the
fraction of the moon visible to Simone on day i) 100 ii) 150 iii)
200
|
|
|
4.
|
The air quality index, I, in a large city can be modelled by the equation
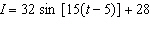 , where t represents the time, in hours, after midnight. New legislation has been
introduced that is expected to decrease the pollution levels in the city so that the index values
will decrease to 90% of current values in 10 years. a) What are the current minimum and
maximum values of the index in the city? b) At what time of the day is the air quality
index at a maximum? c) If an air quality alert is issued for times when the index is above
48, during what time period will an air quality alert be issued? d) What factors in the
equation for air quality index will be affected by the legislation? Explain how they will be
affected. e) What will the new air quality index equation be based on your answers in part
d)? f) How will these changes affect the times when an air quality alert will be
issued?
|
|
|
5.
|
The time, t, in hours, that it takes Alistair to jog 5 km is inversely
proportional to his average speed, v, in kilometres per hour.
a) Write a function
to represent the time as a function of the speed.
b) Sketch the graph of this function.
c) If Alistair jogs at 4.5 km/h, how long does it take him to complete a 5-km run, to the
nearest minute?
|