Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
When a > 0, the function 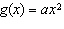 has what relationship to the base
function 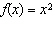 ? A | f(x) is stretched vertically by a factor of |a| and reflected in the
x-axis | B | f(x) is stretched horizontally by a factor of 1/|a| | C | f(x) is
stretched vertically by a factor of |a| | D | f(x) is stretched horizontally by
a factor of 1/|a| and reflected in the y-axis |
|
|
|
2.
|
When the value of a is less than –1, the function 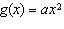
has what relationship to the base function 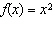 ? A | f(x) is compressed vertically | B | f(x) is
reflected and compressed vertically | C | f(x) is stretched
vertically | D | f(x) is reflected and stretched
vertically |
|
|
|
3.
|
Compared to the graph of the base function 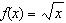 , the graph of the
function 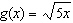 is A | compressed by a factor of 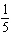 and not reflected and not reflected | B | stretched by a factor
of 5 and reflected in the y-axis | C | compressed by a factor of 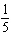 and reflected
in the y-axis and reflected
in the y-axis | D | stretched by a factor of 5 and not reflected |
|
|
|
4.
|
Which radical equation can be solved using the graph shown below? 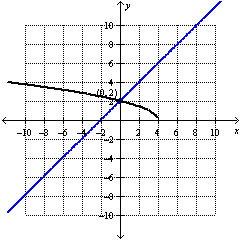
|
|
|
5.
|
Which equation of a radical function would have the following domain and
range? 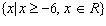 ; 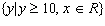
|
|
|
6.
|
What is the maximum number of real distinct roots that a cubic equation can
have?
|
|
|
7.
|
Based on the graph of 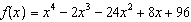 , what are the real roots of 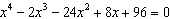 ? 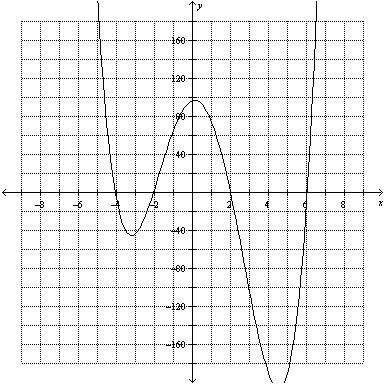 A | –6, –2, 2, 4 | C | there are no real
roots | B | 6, 2, –2, –4 | D | impossible to determine |
|
|
|
8.
|
Determine the equation of a circle with centre at (3, –3) and radius
10.
|
|
|
9.
|
John cuts a slice from a circular ice cream cake with a diameter of 24 cm. His
slice is in the shape of a sector with an arc length of 7 cm. What is the measure of the central
angle of the slice, in radians? Round your answer to two decimal places, if necessary.
A | 1.71 rad | C | 0.29 rad | B | 3.43 rad | D | 0.58 rad |
|
|
|
10.
|
The coordinates of the point that lies at the intersection of the terminal arm
and the unit circle at an angle of 110° are
A | (0.94, –0.34) | C | (–0.34, 0.94) | B | (–0.34, –2.75) | D | (–2.75,
0.94) |
|
|
|
11.
|
Identify a measure for the central angle q in the
interval 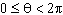 such that point ( 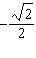 , , 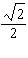 ) is on the terminal arm.
|
|
|
12.
|
Which is a possible value of q, to the nearest
hundredth of a radian, when cos q =
–0.58?
|
|
|
13.
|
The range (in radians) of the graph of 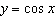 is
|
|
|
14.
|
The period (in degrees) of the graph of 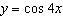 is
|
|
|
15.
|
Which graph represents the function y = 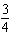 cos( 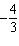 x x),
where x is in degrees?
|
|
|
16.
|
Which function is represented by the graph shown below, where q is in radians?
|
|
|
17.
|
What is the amplitude of the sinusoidal function 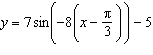 ? A | 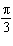 | C | –5 | B | –8 | D | 7 |
|
|
|
18.
|
Determine the phase shift of the sinusoidal function 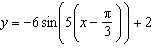 . A | 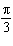 units to the right units to the right | C | 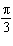 units to the
left units to the
left | B | 3p units to the left | D | 3p units to the
right |
|
|
|
19.
|
Which function represents the graph shown, where x is in radians? 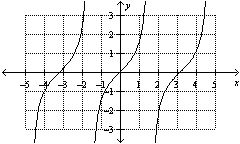
|
|
|
20.
|
Which expression is equivalent to 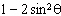 ?
|
|
|
21.
|
Which expression is equivalent to 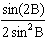 ?
|
|
|
22.
|
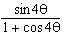 is equivalent to
|
|
|
23.
|
The domain of the function 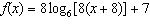 is
|
|
|
24.
|
Compared to the graph of the base function 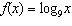 , the graph of the
function 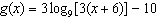 is A | translated down 10 units and left 6 units, horizontally stretched by a factor of 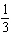 ,
reflected in the y-axis, vertically stretched by a factor of 3, and reflected in the
x-axis ,
reflected in the y-axis, vertically stretched by a factor of 3, and reflected in the
x-axis | C | translated down 10 units and left 6 units, horizontally stretched by a factor of 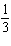 ,
not reflected in the y-axis, vertically stretched by a factor of 3, and not reflected in the
x-axis ,
not reflected in the y-axis, vertically stretched by a factor of 3, and not reflected in the
x-axis | B | translated down 10 units and right 6 units, horizontally stretched by a factor of
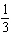 , reflected in the y-axis, vertically stretched by a factor of 3, and not reflected in the
x-axis , reflected in the y-axis, vertically stretched by a factor of 3, and not reflected in the
x-axis | D | translated up 10
units and left 6 units, horizontally stretched by a factor of 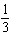 , not reflected in the
y-axis, vertically stretched by a factor of 3, and not reflected in the
x-axis , not reflected in the
y-axis, vertically stretched by a factor of 3, and not reflected in the
x-axis |
|
|
|
25.
|
Which graph represents the function 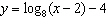 ?
|
|
|
26.
|
Which graph represents the function 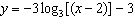 ?
|
|
|
27.
|
If 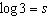 , 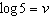 , and 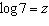 , an algebraic expression
in terms of s, v, and z for 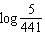 is A | v - 2s + 2z | C | v - 2(s - z) | B | v - 2(s + z) | D | v - 2s
+ z |
|
|
|
28.
|
What is the x-intercept of 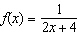 ? A | There is no x-intercept. | C | 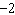 | B | 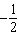 | D | 0 |
|
|
|
29.
|
Given the functions 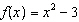 and 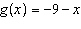 , determine the equation for the combined
function 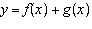 .
|
|
|
For the following question(s), assume that x is in radians, if
applicable.
|
|
|
30.
|
Given the functions 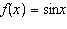 and 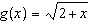 , what is the value of 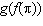 ?
|
|
|
31.
|
Given the functions 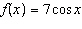 and 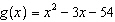 , determine the domain of the combined
function 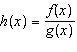 .
|
|
|
32.
|
Given the functions 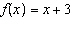 and 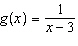 , what is the simplified form of 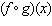 ?
|
|
|
33.
|
Rachael has a digital music player that holds 800 songs. She has 1500 songs in
her music library. She decides that her 50 favourite songs must be on the player. Which expression
can be used to calculate the number of ways can she load songs on to the MP3 player so that it is
full?
|
|
|
34.
|
Which of the following has 30 terms in its binomial expansion?
|
|
|
35.
|
The leadership committee at a high school has 4 grade 10 students, 2 grade 11
students, and 6 grade 12 students. This year, 12 grade 10, 8 grade 11, and 10 grade 12 students
applied for the committee. How many ways are there to select the committee?
A | 2 910 600 | C | 733 | B | 100 590 336 000 | D | 163 136 |
|
Short Answer
|
|
|
1.
|
Create a graph of 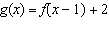 for each base function given, using
transformations. a) 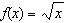 b) b) 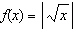
|
|
|
2.
|
Solve the equation 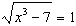 algebraically.
|
|
|
3.
|
Write the equation for the function that results from each transformation or set
of transformations applied to the base function 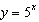 . a) reflect in the
y-axis b) shift 3 units to the right c) shift 1 unit down and 4 units to
the left d) reflect in the x-axis and shift 2 units down
|
|
|
4.
|
Evaluate 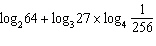 .
|
|
|
5.
|
Given the functions 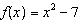 and 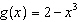 , determine a simplified equation for 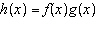 .
|
Problem
|
|
|
1.
|
A windmill has blades that are 20 m in length, and the centre of their circular
motion is a point 23 m above the ground. The blades have a frequency of 4 revolutions per minute when
in operation.
a) Use a sinusoidal function to model the height above the ground of the tip
of one blade as a function of time.
b) Graph the function over three complete
cycles.
c) How far above the ground is the tip of the blade after 10 s?
|
|
|
2.
|
The flapping of a bird’s wing can be modelled by the function 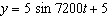 ,
where y represents the distance the tip of the wing travels, in centimetres, and t
represents the time, in seconds. a) Determine the period of the motion of the
wing. b) Determine the amplitude, the minimum value, and the maximum value. c)
What are the first times after t = 0 that the tip of the wing reaches the minimum and maximum
values? d) Determine the position of the wing tip at i) 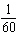
s ii) 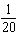 s iii) 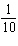 s
|
|
|
3.
|
Wilson places a measuring tape on a pillar of a dock to record the water level
in his local coastal community. He finds that a high tide of 1.77 m occurs at 5:17 a.m., and a low
tide of 0.21 m occurs at 11:38 a.m.
a) Estimate the period of the fluctuation of the water
level.
b) Estimate the amplitude of the pattern.
c) Predict when the next two
high tides will occur.
d) Predict when the next two low tides will occur.
|
|
|
4.
|
If 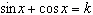 , for what value(s) of k does 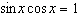 ?
|
|
|
5.
|
The magnitude of an earthquake is defined as 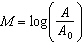 , where A is the
amplitude of the ground motion and 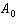 is the amplitude corrected for the distance from the actual
earthquake that would be expected for a “standard earthquake.” On March 2, 2012, an
earthquake with an amplitude 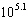 times 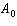 was recorded in Norman Wells, Northwest
Territories. a) What was the earthquake’s magnitude on the Richter
scale? b) How does the earthquake in Norman Wells compare to the earthquake off Vancouver
Island in 1946 that measured 7.3 on the Richter scale?
|