Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Which of the following functions is the correct inverse for the function 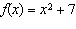 ,
{ x | x ³ 0, x Î R}?
|
|
|
2.
|
Which of the following relations is the correct inverse for the function 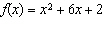 ?
|
|
|
3.
|
Which graph represents the inverse of the function shown? 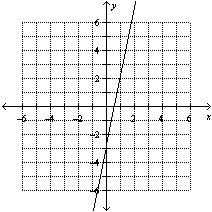
|
|
|
4.
|
Compared to the graph of the base function 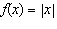 , the graph of the
function 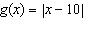 is translated A | 10 units up | C | 10 units down | B | 10 units to the left | D | 10 units to the
right |
|
|
|
5.
|
Given the graph of f( x) shown below, what are the coordinates of
point A if the transformed graph is represented by 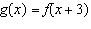 ? 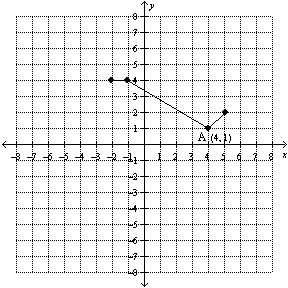
|
|
|
6.
|
When a > 0, the function 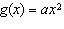 has what relationship to the base
function 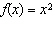 ? A | f(x) is stretched horizontally by a factor of 1/|a| | B | f(x) is
stretched horizontally by a factor of 1/|a| and reflected in the y-axis | C | f(x) is
stretched vertically by a factor of |a| | D | f(x) is stretched vertically by a
factor of |a| and reflected in the x-axis |
|
|
|
7.
|
When b > 0, the function 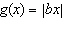 has what relationship to the base
function 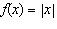 ? A | f(x) is stretched horizontally by a factor of 1/|b| | B | f(x) is
stretched vertically by a factor of |b| | C | f(x) is stretched vertically by a
factor of |b| and reflected in the x-axis | D | f(x) is stretched horizontally by
a factor of 1/|b| and reflected in the y-axis |
|
|
|
8.
|
Which of the graphs shown below represents the base function 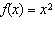 and the
stretched function g( x) = 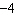 x2 x2?
|
|
|
9.
|
What are the coordinates of the invariant point(s) when the function 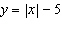 is
reflected in the x-axis? A | (–5, 0) and (5, 0) | C | (0, –5) | B | (5,
–5) | D | (0,
5) |
|
|
|
10.
|
Compared to the graph of the base function 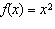 , the graph of the function
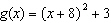 is translated A | 3 units to the left and 8 units up | C | 3 units to the right and 8 units
down | B | 8 units to the right and 3 units down | D | 8 units to the left and 3 units
up |
|
Short Answer
|
|
|
1.
|
For each g( x), describe the transformation(s) from the base
function 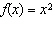 . a) 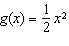 b) b) 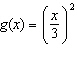 c) c) 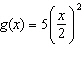
|
|
|
2.
|
For each g( x), describe, in the appropriate order, the combination
of transformations that must be applied to the base function 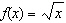 . a) 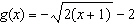 b) b) 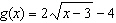 c) c) 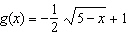
|
Problem
|
|
|
1.
|
Consider the function 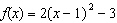 . a) Determine the equation of
each function. i) 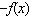 ii) f ii) f(– x) iii) 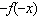 b) b) Graph all four functions from part a) on the same set of axes. c)
From the graph, determine the pairs of equations that can be represented as translations of each
other. d) Describe the translation that can be applied to each pair of functions you
determined in part c) to generate the same graph.
|
|
|
2.
|
An object falls to the ground from a height of 25 m. The height, h, in
metres, of the object above the ground can be modelled by the function 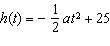 , where a is the
acceleration due to gravity, in metres per second squared, and t is the time, in
seconds. a) Write an equation for the height of the object on Earth given a = 9.8
m/s 2. b) Write an equation for the height of the object on Mars given a =
3.7 m/s 2. c) Graph both functions on the same set of axes. d) What
scale factor can be applied to the Earth function to transform it to the Mars function?
|
|
|
3.
|
The equation 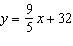 can be used to convert between Celsius and Fahrenheit
temperatures, where x is the temperature in degrees Celsius and y is the temperature in
degrees Fahrenheit. a) Determine the inverse of this equation. What does it represent? What
do the variables represent? b) Graph the original and inverse functions on the same set of
axes. c) Which temperature is the same in Celsius and Fahrenheit? Explain how you
know.
|