Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Which graph represents an odd-degree polynomial function with two
x-intercepts?
|
|
|
2.
|
Which graph represents an even-degree polynomial function with a
y-intercept of 9?
|
|
|
3.
|
How many x-intercepts are possible for the polynomial function 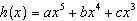 ?
|
|
|
4.
|
If 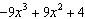 is divided by 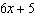 , then the restriction on x
is
|
|
|
5.
|
What is the remainder when 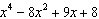 is divided by 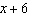 ?
|
|
|
6.
|
If 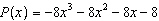 is divided by 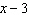 , what is the
remainder?
|
|
|
7.
|
If 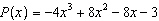 is divided by 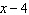 , what is the remainder? A | P(x – 4) | C | P(x +
4) | B | P(4) | D | P(–4) |
|
|
|
8.
|
Determine the value of k so that 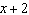 is a factor of 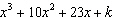 . A | k = –1 | C | k = 14 | B | k = –14 | D | k = 1 |
|
|
|
9.
|
One root of the equation 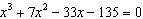 is
|
|
|
10.
|
The graph that corresponds to the function 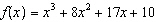 is
|
Short Answer
|
|
|
1.
|
a) Use long division to divide x3 +
3x2 – 7 by x + 2. Express the result in quotient form.
b)
Identify any restrictions on the variable.
c) Write the corresponding statement that can be
used to check the division.
d) Verify your answer.
|
|
|
2.
|
Factor fully.
a) –n3 –
4n2 – 4n
b) 12x3 + 16x2
– 5x – 3
c) 2x4 + x3 –
10x – 5
|
|
|
3.
|
Solve.
a) 3x3 + 2x2 –
8x + 3 = 0
b) 2x3 + x2 – 10x
– 5 = 0
c) 5x4 = 7x2 – 2
|
Problem
|
|
|
1.
|
a) If x + 1 is a factor of ax4 +
bx2 + c, what is the value of a + b + c?
b)
Decide if x + 1 is a factor of each polynomial. Explain your
reasoning.
i) 3x4 + 3x2
– 6
ii) 17x4 –
10x2 – 7
iii)
x4 + x2 + 1
|
|
|
2.
|
Maria is designing a series of stationery trays for holding paper and envelopes.
Each tray starts as a rectangular sheet of metal from which identical squares are cut from the four
corners. The resulting rectangular flaps are then folded up and welded to produce an open-topped
rectangular tray. What size square should Maria cut from a rectangular sheet of metal 15 cm by 25 cm
in order to produce a tray with a volume of 476 cm3? Round to the nearest hundredth of a
centimetre, if necesary.
|
|
|
3.
|
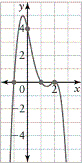
Determine an equation in factored form for the polynomial function represented
by the graph
|