Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Which of the following is a polynomial function?
|
|
|
2.
|
Which graph represents an even-degree polynomial function with a
y-intercept of 4?
|
|
|
3.
|
How many x-intercepts are possible for the polynomial function  ?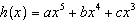
|
|
|
4.
|
If 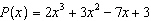 is divided by 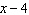 , what is the
remainder?
|
|
|
5.
|
If 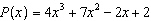 is divided by 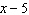 , what is the remainder? A | P(x + 5) | C | P(5) | B | P(x – 5) | D | P(–5) |
|
|
|
6.
|
A factor of 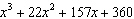 is A | 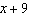 | C | x –
5 | B | 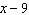 | D | x –
8 |
|
|
|
7.
|
Determine the value of k so that 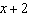 is a factor of 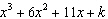 . A | k = –1 | C | k = –6 | B | k = 1 | D | k = 6 |
|
|
|
8.
|
The fully factored form of 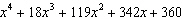 is
|
|
|
9.
|
What is the maximum number of real distinct roots that a quadratic equation can
have?
|
|
|
10.
|
Given the function 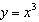 , what are the parameters of the transformed function
y = 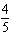 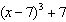 and what is the effect of each parameter on the graph of
the original function? A | a = 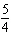 , vertical stretch about the x-axis by a factor of
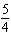
h = 7, horizontal translation 7 units right
k = 7, vertical
translation 7 units right | B | a = 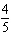 , vertical stretch about
the x-axis by a factor of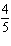 
h = 7, horizontal translation 7 units
right
k = 7, vertical translation 7 units right | C | a =  ,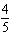
vertical stretch about the x-axis by a factor of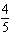 
h = 7, horizontal translation 7
units right
k = 7, vertical translation 7 units right | D | a =  ,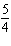
vertical stretch about the x-axis by a factor of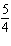 
h = 7, horizontal translation
7 units left
k = 7, vertical translation 7 units down |
|
Short Answer
|
|
|
1.
|
Factor fully.
a) –n3 –
4n2 – 4n
b) 12x3 + 16x2
– 5x – 3
c) 2x4 + x3 –
10x – 5
|
|
|
2.
|
Factor fully.
a) x2(x – 2)(x +
2) + 3x + 6
b) 16x4 – (x + 1)2
|
|
|
3.
|
Determine the degree of the polynomial function (linear, quadratic, cubic, etc.)
that the table of values represents. x | y | –3 | | 7 | | –2 | | 9 | | –1 | | 5 | | 0 | | 1 | | 1 | | 3 | | 2 | | 17 | | 3 | | 49 | | | | | |
|
Problem
|
|
|
1.
|
The polynomial 6x3 + mx2 + nx –
5 has a factor of x + 1. When divided by x – 1, the remainder is –4. What
are the values of m and n?
|
|
|
2.
|
a) If x + 1 is a factor of ax4 +
bx2 + c, what is the value of a + b + c?
b)
Decide if x + 1 is a factor of each polynomial. Explain your
reasoning.
i) 3x4 + 3x2
– 6
ii) 17x4 –
10x2 – 7
iii)
x4 + x2 + 1
|
|
|
3.
|
Prove that x2 + 5x + 6 is a factor of
x4 + 5x3 + 2x2 – 20x –
24.
|