Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Compared to the graph of the base function 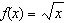 , the graph of the
function 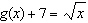 is translated A | 7 units to the right | C | 7 units up | B | 7 units to the left | D | 7 units down |
|
|
|
2.
|
Compared to the graph of the base function 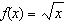 , the graph of the
function 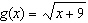 is translated A | 9 units down | C | 9 units right | B | 9 units left | D | 9 units up |
|
|
|
3.
|
Given the function 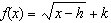 with a domain of 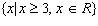 and a range of 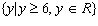 , which of the
following best describes the vertical and horizontal translations with respect to the graph of 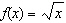 ? A | 3 units to the right and 6 units up | C | 3 units to the right and 6 units
down | B | 6 units to the right and 3 units down | D | 6 units to the right and 3 units
up |
|
|
|
4.
|
Compared to the graph of the base function 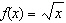 , the graph of the function
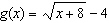 is translated A | 8 units to the left and 4 units down | C | 4 units to the right and 8 units
up | B | 4 units to the left and 8 units down | D | 8 units to the right and 4 units
up |
|
|
|
5.
|
What is the equation of the radical function shown in the graph below? 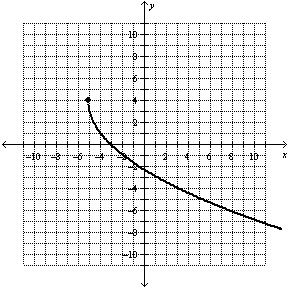
|
|
|
6.
|
What are the coordinates of the invariant point(s) when the function 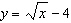 is
reflected in the x-axis? A | (16, –4) | C | (0, 16) | B | (0, –4) | D | (16, 0) |
|
|
|
7.
|
What is the solution to the radical equation 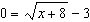 ?
|
|
|
8.
|
Which graph represents an odd-degree polynomial function with two
x-intercepts?
|
|
|
9.
|
How many x-intercepts are possible for the polynomial function 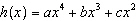 ?
|
|
|
10.
|
What is the restriction on x if 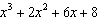 is divided by 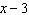 ?
|
|
|
11.
|
If 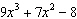 is divided by 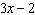 , then the restriction on x
is
|
|
|
12.
|
If 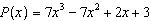 is divided by 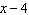 , what is the
remainder?
|
|
|
13.
|
If 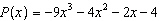 is divided by 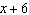 , what is the remainder? A | P(6) | C | P(x + 6) | B | P(–6) | D | P(x – 6) |
|
|
|
14.
|
When 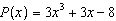 is divided by 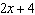 , the remainder is
|
|
|
15.
|
One root of the equation 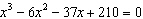 is
|
Short Answer
|
|
|
1.
|
Sketch the graph of 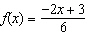 and use it to sketch the graph of 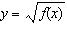 .
|
|
|
2.
|
Solve the equation 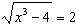 graphically.
|
|
|
3.
|
Factor fully.
a) x3 + 6x2 +
11x + 6
b) 4x3 – 11x2 –
3x
c) x4 – 81
|
|
|
4.
|
Factor fully.
a) –n3 –
4n2 – 4n
b) 12x3 + 16x2
– 5x – 3
c) 2x4 + x3 –
10x – 5
|
|
|
5.
|
Factor 2x3 + 5x2 – 14x
– 8 fully
|
Problem
|
|
|
1.
|
Graph the functions below, and then identify and compare their domains and
ranges. 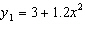 and 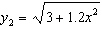
|
|
|
2.
|
Sun-Eui, a graduate student, is using the function 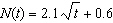 to model the number of
flowers a new hybrid bee can pollinate. For the function, N represents the number, in
thousands, of flowers pollinated and t represents the time, in days. a) If there are
10 000 flowers, how long will it take to pollinate all of the flowers? b) Sun-Eui believes
that the second generation of bees can reduce the time to pollinate the flowers by half by changing
the function to 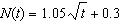 . Is she correct? Justify your reasoning. c)
Should Sun-Eui continue with the project?
|
|
|
3.
|
The polynomial 6x3 + mx2 + nx –
5 has a factor of x + 1. When divided by x – 1, the remainder is –4. What
are the values of m and n?
|
|
|
4.
|
a) If x + 1 is a factor of ax4 +
bx2 + c, what is the value of a + b + c?
b)
Decide if x + 1 is a factor of each polynomial. Explain your
reasoning.
i) 3x4 + 3x2
– 6
ii) 17x4 –
10x2 – 7
iii)
x4 + x2 + 1
|
|
|
5.
|
Prove that x2 + 5x + 6 is a factor of
x4 + 5x3 + 2x2 – 20x –
24.
|