Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
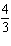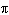  radians is equal to how many degrees?
|
|
|
2.
|
The exact radian measure for an angle of 255° is
|
|
|
3.
|
Determine the arc length of a circle with radius 5.5 cm if it is subtended by a
central angle of 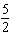 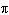 radians. Round your answer to one
decimal place. A. | 1.4 cm | C. | 4.4 cm | B. | 43.2 cm | D. | 6.9 cm |
|
|
|
4.
|
Determine the equation of a circle with centre at (3, –3) and radius
10.
|
|
|
5.
|
John cuts a slice from a circular ice cream cake with a diameter of 24 cm. His
slice is in the shape of a sector with an arc length of 7 cm. What is the measure of the central
angle of the slice, in radians? Round your answer to two decimal places, if necessary.
A. | 1.71 rad | C. | 0.29 rad | B. | 3.43 rad | D. | 0.58 rad |
|
|
|
6.
|
Identify the point on the unit circle corresponding to an angle of 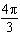 radians in standard position.
|
|
|
7.
|
During a routine, a figure skater completes 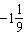 rotations. How many
degrees has the figure skater turned? A. | –400° | C. | –220° | B. | 400° | D. | 580° |
|
|
|
8.
|
A tricycle has a front wheel that is 30 cm in diameter and two rear wheels that
are each 12 cm in diameter. If the front wheel rotates through a angle of 32°, through how many
degrees does each rear wheel rotate, to the nearest tenth of a degree?
A. | 32.0° | C. | 80.0Á | B. | 40.0Á | D. | 160.0Á |
|
|
|
9.
|
The point P(0.391, 0.921) is the point of intersection of a unit circle and the
terminal arm of an angle q in standard position. What is the equation of
the line passing through the centre of the circle and the point P? Round the slope to two decimal
places.
|
|
|
10.
|
A bottle is riding the waves at a beach. The bottle’s
up and down motion with the waves can be described using the formula 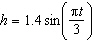 , where h is the
height, in metres, above the flat water surface and t is the time, in seconds. When is the
first time, to the nearest tenth of a second, that the height of the bottle will be 1.4
m?
A. | 14.8 s | C. | 0.9
s | B. | 1.1 s | D. | 1.5
s |
|
Short Answer
|
|
|
1.
|
Find the exact value of  .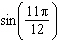
|
|
|
2.
|
Determine the exact measures for all angles where 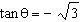 in
the domain  .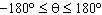
|
Problem
|
|
|
1.
|
Two wires are connected to a tower at the same point on the tower. Wire #1 makes
an angle of 45° with the ground and wire #2 makes an angle of 60° with the
ground.
a) Represent this situation with a diagram.
b) Which wire is longer?
Explain.
c) If the point where the two wires connect to the tower is 35 m above the ground,
determine exact expressions for the lengths of the two wires.
d) Determine the length of
each wire, to the nearest tenth of a metre.
e) How do your answers to parts b) and d)
compare?
|
|
|
2.
|
Sarah and Simone are walking in a walk-a-thon down a straight street that leads
to the finish line in the park. At the same time, they both notice a hot-air balloon directly over
the finish line. Sarah sees the angle from the ground to the balloon as 30° and Simone, who is
0.25 km closer to the finish line than Sarah, sees the angle from the ground to the balloon as
45°.
a) Draw a diagram to represent this situation.
b) If x
represents the distance that Simone is from the finish line, write an expression for the distance
from Sarah to the finish line.
c) Write a trigonometric ratio for each girl’s
position that involves the height of the balloon, h; the distance, x, each girl is away
from the finish line; and the angle from the girl to the balloon.
d) Rearrange each
equation from part c) to isolate h.
e) Set the two expressions for h equal to
each other and solve for x, to the nearest hundredth of a kilometre.
f) Determine
the height of the balloon, to the nearest hundredth of a kilometre.
|
|
|
3.
|
Jason is standing 8.7 km from town X and 11.5 km from town Y. From where he
stands, the angle between the two towns is 37°. A new hotel has just been built on the road
connecting town X and town Y, exactly halfway between the two towns. From where Jason is standing, he
sees that the angle of elevation to the top of the hotel is 1°. Determine the height of the
hotel, to the nearest tenth of a metre. Include a diagram with your solution.
|