Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
The exact radian measure for an angle of 255° is
|
|
|
2.
|
Determine the equation of a circle with centre at the origin and radius
8.
|
|
|
3.
|
Determine the equation of a circle with centre at (3, –3) and radius
10.
|
|
|
4.
|
Which graph represents an angle in standard position with a measure of 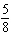 p p rad?
|
|
|
5.
|
Determine the measure of the angle in standard position shown on the graph
below. Round your answer to the nearest tenth of a degree. A. | 161.6° | C. | 71.6° | B. | 341.6° | D. | 251.6° |
|
|
|
6.
|
John cuts a slice from a circular ice cream cake with a diameter of 24 cm. His
slice is in the shape of a sector with an arc length of 7 cm. What is the measure of the central
angle of the slice, in radians? Round your answer to two decimal places, if necessary.
A. | 1.71 rad | C. | 0.29 rad | B. | 3.43 rad | D. | 0.58 rad |
|
|
|
7.
|
Which point on the unit circle corresponds to tan
q = 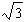 ? ?
|
|
|
8.
|
Which is a possible value of q, to the nearest
hundredth of a radian, when cos q =
–0.58?
A. | –2.19 | C. | 2.19 | B. | –0.62 | D. | 0.84 |
|
|
|
9.
|
If the angle q is –5000° in standard
position, it can be described as having made
A. | 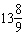 rotations rotations | C. | 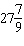 rotations
rotations | B. | 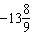 rotations rotations | D. | 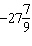 rotations rotations |
|
|
|
10.
|
The point P(0.391, 0.921) is the point of intersection of a unit circle and the
terminal arm of an angle q in standard position. What is the equation of
the line passing through the centre of the circle and the point P? Round the slope to two decimal
places.
|
Short Answer
|
|
|
1.
|
Find the exact value of 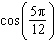 .
|
|
|
2.
|
Without using a calculator, determine two angles between 0° and 360°
that have a cosecant of 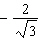 . Include an explanation of how you determined the two
angles.
|
Problem
|
|
|
1.
|
In DABC, c = 11 cm, b = 7 cm, and ÐB = 38°.
a) Sketch possible diagrams for this
situation.
b) Determine the measure, to the nearest degree, of ÐC in each diagram.
c) Find the measure of ÐA in each diagram.
d) Calculate the length of BC in each
diagram.
|
|
|
2.
|
a) For the given trigonometric ratio, determine two other angles that
have the same value.
i) sin 45°
ii) tan 300°
iii) cos
120°
b) Explain how you determined the angles in part a).
|
|
|
3.
|
A bicycle tire revolves at 150 rpm (revolutions per minute). What is its angular
velocity, in radians per second, rounded to two decimal places?
|