Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Which function, where x is in radians, is represented by the graph shown
below? 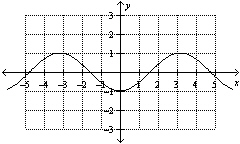
|
|
|
2.
|
The range (in radians) of the graph of 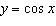 is
|
|
|
3.
|
The period (in degrees) of the graph of 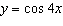 is
|
|
|
4.
|
The amplitude and period (in degrees) of 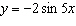 are A. | amplitude = 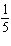
period = 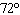 | C. | amplitude = 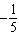
period =
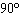 | B. | amplitude = 2
period = 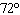 | D. | amplitude = –2
period = 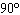 |
|
|
|
5.
|
What is the period of the sinusoidal function 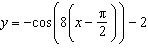 ?
|
|
|
6.
|
Which graph represents the sinusoidal function 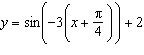 ?
|
|
|
7.
|
What are the solutions for 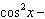 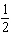 = 0 in the interval 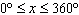 ? A. | x = 90° and 270° 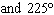 | C. | x = 60° and 240° and 45° | B. | 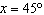 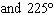 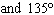 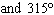 | D. | x =
30° and 210° 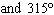 |
|
|
|
Use the following information to answer the questions.The height,
h, in centimetres, of a piston moving up and down in an engine cylinder can be modelled by the
function 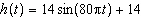 , where t is the time, in seconds.
|
|
|
8.
|
What is the piston’s minimum height?
A. | 14 cm | C. | 0 cm | B. | –14 cm | D. | 7 cm |
|
|
|
9.
|
What is the period?
|
|
|
10.
|
Solve 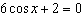 to three decimal places on the interval 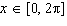 . A. | x = 0.340, x = 5.943 | C. | x = 1.911, x =
1.231 | B. | x = 1.231, x = 5.052 | D. | x = 1.911, x =
4.373 |
|
Short Answer
|
|
|
1.
|
Solve 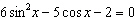 on the interval 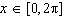 .
|
|
|
2.
|
Sketch the graph of 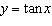 for two cycles and state the domain, range, period, and
equations of the asymptotes. x is measured in radians.
|
Problem
|
|
|
1.
|
Sketch the graph of 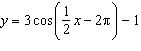 for 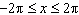 .
|
|
|
2.
|
A mass is suspended by a spring such that it hangs at rest 0.5 m above the
ground. The mass is raised 40 cm and released at time t = 0 s, causing it to oscillate
sinusoidally. If the mass returns to the high position every 1.2 s, determine the height of the mass
above the ground at t = 0.7 s.
|
|
|
3.
|
A cosine function has half the period of the function 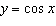 . All other
properties of the two functions are identical. a) Determine the number of points of
intersection if these two functions are graphed on the interval 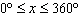 . Explain. b)
Determine the values of x of the first two points of intersection to the right of x =
0°. c) If the graph of the two functions were extended to 720°, how many points
of intersection would there be? Explain. d) Use the concept of coterminal angles to
determine the values of x where the points of intersection would occur. e) Graph the
two functions over the interval 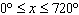 to verify your answer for parts b), c), and d).
|