Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
The range (in radians) of the graph of 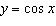 is
|
|
|
2.
|
The period (in degrees) of the graph of 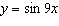 is
|
|
|
3.
|
The amplitude and period (in degrees) of 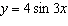 are A. | amplitude = 4
period = 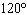 | C. | amplitude = –4
period =
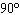 | B. | amplitude = 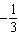
period = 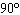 | D. | amplitude = 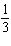
period = 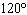 |
|
|
|
4.
|
Which function is represented by the graph shown below, where x is in
degrees?
|
|
|
5.
|
What is the amplitude of the sinusoidal function 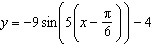 ? A. | 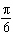 | C. | 9 | B. | –4 | D. | 5 |
|
|
|
6.
|
Which graph represents the sinusoidal function 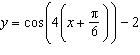 ?
|
|
|
7.
|
Which graph represents the sinusoidal function 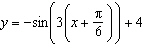 ?
|
|
|
8.
|
Which function represents the graph shown, where x is in radians? 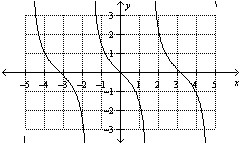
|
|
|
9.
|
Given the trigonometric function 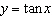 , find the value of the
y-coordinate of the point with x-coordinate –855°.
|
|
|
10.
|
Solve 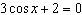 , to the nearest tenth of a degree, if necessary, on the
interval 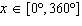 . A. | x = 131.8°, x = 48.2° | C. | x = 41.8°, x =
318.2° | B. | x = 131.8°, x = 228.2° | D. | x = 48.2°, x = 311.8° |
|
Short Answer
|
|
|
1.
|
A population, p, of bears varies according to 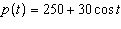 , where
t is the time, in years, and angles are measured in radians. a) What are the maximum
and minimum populations? b) What is the first interval, in years and months, over which the
population is increasing?
|
|
|
2.
|
A girl jumps rope such that the height, h, in metres, of the middle of
the rope can be approximated by the equation 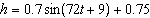 , where t is the time, in
seconds. a) What is the amplitude of this function? b) How many revolutions of
the rope does the girl make in 1 min?
|
Problem
|
|
|
1.
|
The table shows the fraction of the Moon that can be seen at midnight from
Simone’s town. Day 1 represents January 1. Day | 1 | 2 | 3 | 4 | 5 | 6 | 10 | 14 | 19 | 21 | Fraction
Visible | 0.25 | 0.17 | 0.12 | 0.06 | 0.02 | 0.00 | 0.10 | 0.56 | 0.98 | 1.00 | | | | | | | | | | | |
| Day | 24 | 30 | 35 | 41 | 45 | 51 | 56 | 60 | 65 | 66 | Fraction
Visible | 0.78 | 0.33 | 0.02 | 0.15 | 0.65 | 1.00 | 0.78 | 0.30 | 0.01 | 0.00 | | | | | | | | | | | |
a) What is the period of the sine function that could be used to
model the data? b) What is the amplitude of the function? c) What is the phase
shift of the function? d) What is the vertical shift? e) Use your answers to
parts a) to d) to write an equation for the function. f) Use your function to determine the
fraction of the moon visible to Simone on day i) 100 ii) 150 iii)
200
|
|
|
2.
|
George sells new cars at a local dealership. The table shows the number of cars
sold by George each month for a year. Note that month 1 corresponds to January. Month | Number
of New Cars Sold | 1 | 5 | 2 | | 3 | 20 | 4 | 30 | 5 | 37 | 6 | 39 | 7 | 36 | 8 | 30 | 9 | 19 | 10 | 10 | 11 | 4 | 12 | 2 | | |
a) Use the table to determine a
function that can be used to model the information. b) Over what domain and range is this
model valid? c) The value for the second month is missing. Use your model to determine how
many cars George sold in that month. d) Do you expect the data to continue to be
sinusoidal? Explain.
|
|
|
3.
|
The flapping of a bird’s wing can be modelled by the function 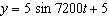 ,
where y represents the distance the tip of the wing travels, in centimetres, and t
represents the time, in seconds. a) Determine the period of the motion of the
wing. b) Determine the amplitude, the minimum value, and the maximum value. c)
What are the first times after t = 0 that the tip of the wing reaches the minimum and maximum
values? d) Determine the position of the wing tip at i) 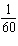
s ii) 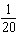 s iii) 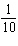 s
|