Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
The graph of 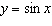 can be obtained by translating the graph of 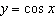 A. | 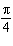 units to the right units to the right | C. | 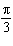 units to the
right units to the
right | B. | 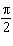 units to the right units to the right | D. | 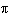 units to the
right units to the
right |
|
|
|
2.
|
Which of the following is not an asymptote of the function 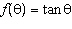 ?
|
|
|
3.
|
Which function has zeros only at 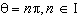 ? A. | y = tan(q 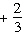 p) p) | C. | y =
tan(q 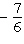 p) p) | B. | 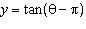 | D. | y = tan(q 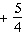 p) p) |
|
|
|
Use the following information to answer the questions.The height,
h, in metres, above the ground of a car as a Ferris wheel rotates can be modelled by the
function 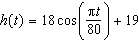 , where t is the time, in seconds.
|
|
|
4.
|
What is the radius of the Ferris wheel?
|
|
|
5.
|
How long does it take for the wheel to revolve once?
A. | 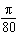 s s | C. | 160 s | B. | 80
s | D. | 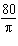 s
s |
|
|
|
6.
|
What is the minimum height of a car?
|
|
|
7.
|
What is the maximum height of a car?
A. | 19 m | C. | 160 m | B. | 80 m | D. | 31 m |
|
|
|
8.
|
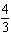 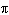 radians is equal to how many degrees?
|
|
|
9.
|
If the angle q is 1600° in standard position, in
which quadrant does it terminate?
A. | quadrant III | C. | quadrant II | B. | quadrant IV | D. | quadrant I |
|
|
|
10.
|
The range (in radians) of the graph of 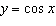 is
|
|
|
11.
|
What is the period of the sinusoidal function 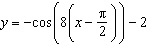 ?
|
|
|
12.
|
Given the trigonometric function 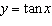 , which is the x-coordinate at
which the function is undefined?
|
|
|
13.
|
Given the trigonometric function 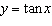 , find the value of the
y-coordinate of the point with x-coordinate –1200°.
|
|
|
14.
|
What are the solutions for 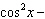 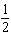 = 0 in the interval 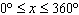 ? A. | x = 90° and 270° 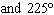 | C. | x = 60° and 240° and 45° | B. | 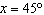 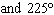 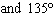 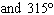 | D. | x =
30° and 210° 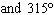 |
|
|
|
Use the following information to answer the questions.The height,
h, in centimetres, of a piston moving up and down in an engine cylinder can be modelled by the
function 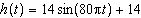 , where t is the time, in seconds.
|
|
|
15.
|
What is the period?
|
Short Answer
|
|
|
1.
|
Explain how you could graph the function 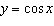 given a table of values
containing ordered pairs for the function 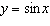 .
|
|
|
2.
|
Solve 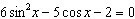 on the interval 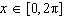 .
|
|
|
3.
|
The water level at an ocean inlet has a depth, d, in metres, that varies
with the time, t, in hours after midnight, according to the equation 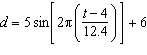 . What is the
water depth at 2:30 a.m., to the nearest hundredth of a metre?
|
|
|
4.
|
Describe the transformations that, when applied to the graph of y = cos
x, result in the graph of 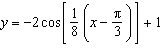 .
|
|
|
5.
|
A pebble is embedded in the tread of a rotating bicycle wheel of diameter 60 cm.
If the wheel rotates at 4 revolutions per second, determine a relationship between the height,
h, in centimetres, of the pebble above the ground as a function of time, t, in
seconds.
|
Problem
|
|
|
1.
|
The table shows the hours of daylight measured on the first day of each month,
over a 1-year period in a northern Ontario city. Month | Hours of Daylight (h:min) | 1 | 8:25 | 2 | 9:55 | 3 | 11:35 | 4 | 13:30 | 5 | 15:48 | 6 | 16:15 | 7 | 15:25 | 8 | 14:26 | 9 | 12:35 | 10 | 10:39 | 11 | 9:01 | 12 | 8:00 | | |
a) Graph the table data. b) Use
the graph and the table to develop a sinusoidal model to represent the information. c)
Graph the model on the same set of axes as the data. Comment on the fit. d) Use your model
to estimate the number of hours of daylight, to the nearest tenth of an hour, on January 15, and
verify the solution using the graph.
|
|
|
2.
|
The table shows the fraction of the Moon that can be seen at midnight from
Simone’s town. Day 1 represents January 1. Day | 1 | 2 | 3 | 4 | 5 | 6 | 10 | 14 | 19 | 21 | Fraction
Visible | 0.25 | 0.17 | 0.12 | 0.06 | 0.02 | 0.00 | 0.10 | 0.56 | 0.98 | 1.00 | | | | | | | | | | | |
| Day | 24 | 30 | 35 | 41 | 45 | 51 | 56 | 60 | 65 | 66 | Fraction
Visible | 0.78 | 0.33 | 0.02 | 0.15 | 0.65 | 1.00 | 0.78 | 0.30 | 0.01 | 0.00 | | | | | | | | | | | |
a) What is the period of the sine function that could be used to
model the data? b) What is the amplitude of the function? c) What is the phase
shift of the function? d) What is the vertical shift? e) Use your answers to
parts a) to d) to write an equation for the function. f) Use your function to determine the
fraction of the moon visible to Simone on day i) 100 ii) 150 iii)
200
|
|
|
3.
|
George sells new cars at a local dealership. The table shows the number of cars
sold by George each month for a year. Note that month 1 corresponds to January. Month | Number
of New Cars Sold | 1 | 5 | 2 | | 3 | 20 | 4 | 30 | 5 | 37 | 6 | 39 | 7 | 36 | 8 | 30 | 9 | 19 | 10 | 10 | 11 | 4 | 12 | 2 | | |
a) Use the table to determine a
function that can be used to model the information. b) Over what domain and range is this
model valid? c) The value for the second month is missing. Use your model to determine how
many cars George sold in that month. d) Do you expect the data to continue to be
sinusoidal? Explain.
|
|
|
4.
|
The flapping of a bird’s wing can be modelled by the function 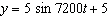 ,
where y represents the distance the tip of the wing travels, in centimetres, and t
represents the time, in seconds. a) Determine the period of the motion of the
wing. b) Determine the amplitude, the minimum value, and the maximum value. c)
What are the first times after t = 0 that the tip of the wing reaches the minimum and maximum
values? d) Determine the position of the wing tip at i) 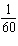
s ii) 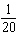 s iii) 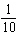 s
|
|
|
5.
|
A sinusoidal function has an amplitude of 2, a period of 180°, and a
maximum at (0, 4).
a) Represent this function with an equation using a sine
function.
b) Represent this function with an equation using a cosine function.
c)
Explain how these two functions are related.
|