Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
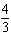 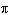 radians is equal to how many degrees?
|
|
|
2.
|
The exact radian measure for an angle of 255° is
|
|
|
3.
|
Which graph represents an angle in standard position with a measure of 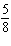 p p rad?
|
|
|
4.
|
Which graph represents an angle in standard position with a measure of
135°?
|
|
|
5.
|
The coordinates of the point that lies at the intersection of the terminal arm
and the unit circle at an angle of 110° are
A. | (0.94, –0.34) | C. | (–0.34, 0.94) | B. | (–0.34, –2.75) | D. | (–2.75,
0.94) |
|
|
|
6.
|
Which is a possible value of q, to the nearest
hundredth of a radian, when cos q =
–0.58?
A. | –2.19 | C. | 2.19 | B. | –0.62 | D. | 0.84 |
|
|
|
7.
|
If the angle q is –5000° in standard
position, it can be described as having made
A. | 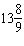 rotations rotations | C. | 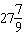 rotations
rotations | B. | 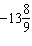 rotations rotations | D. | 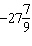 rotations rotations |
|
|
|
8.
|
During a routine, a figure skater completes 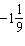 rotations. How many
degrees has the figure skater turned? A. | –400° | C. | –220° | B. | 400° | D. | 580° |
|
|
|
9.
|
Determine the point in quadrant II where the line represented by 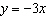 intersects the
unit circle. A. | (0.95, –0.32) | C. | (–0.35, 0.94) | B. | (–0.32, 0.95) | D. | (–0.32,
0.94) |
|
|
|
10.
|
Giai got an answer of 3.86 when she was calculating the value of a trigonometric
function. Assuming Giai did her calculation correctly, which of the following was she
calculating?
A. | tan 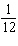 p p | C. | csc 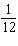 p p | B. | sec 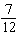 p p | D. | cot
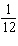 p p |
|
|
|
11.
|
A bottle is riding the waves at a beach. The bottle’s
up and down motion with the waves can be described using the formula 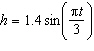 , where h is the
height, in metres, above the flat water surface and t is the time, in seconds. When is the
first time, to the nearest tenth of a second, that the height of the bottle will be 1.4
m? , where h is the
height, in metres, above the flat water surface and t is the time, in seconds. When is the
first time, to the nearest tenth of a second, that the height of the bottle will be 1.4
m?
A. | 14.8 s | C. | 0.9
s | B. | 1.1 s | D. | 1.5
s |
|
|
|
12.
|
The range (in radians) of the graph of 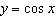 is
|
|
|
13.
|
Given the trigonometric function 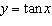 , find the value of the
y-coordinate of the point with x-coordinate –1200°.
|
|
|
14.
|
What are the solutions for 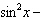 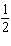 = 0 in the interval 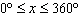 ? A. | 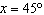 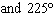 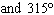 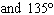 | C. | x = 90° and 270° 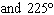 | B. | x = 30° and 210° 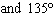 | D. | x = 60°
and 240° and 45°
|
|
|
|
15.
|
Solve 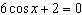 to three decimal places on the interval 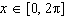 . A. | x = 0.340, x = 5.943 | C. | x = 1.911, x =
1.231 | B. | x = 1.231, x = 5.052 | D. | x = 1.911, x =
4.373 |
|
Short Answer
|
|
|
1.
|
Without using a calculator, determine two angles between 0° and 360°
that have a cosecant of 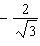 . Include an explanation of how you determined the two
angles.
|
|
|
2.
|
Determine the exact measures for all angles where 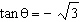 in
the domain in
the domain 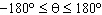 . .
|
|
|
3.
|
The water level at an ocean inlet has a depth, d, in metres, that varies
with the time, t, in hours after midnight, according to the equation 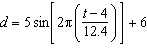 . What is the
water depth at 2:30 a.m., to the nearest hundredth of a metre?
|
|
|
4.
|
Sketch the graph of 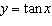 for two cycles and state the domain, range, period, and
equations of the asymptotes. x is measured in radians.
|
|
|
5.
|
A girl jumps rope such that the height, h, in metres, of the middle of
the rope can be approximated by the equation 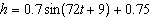 , where t is the time, in
seconds. a) What is the amplitude of this function? b) How many revolutions of
the rope does the girl make in 1 min?
|
Problem
|
|
|
1.
|
To support a new 2.5-m wall in the construction of a home, the carpenters nail a
piece of wood from the top of the wall to the floor, with the piece of wood forming the hypotenuse of
the right triangle it makes with the wall and floor. The piece of wood is nailed to the ground such
that it makes a 30° angle with the floor.
a) Represent this situation with a
diagram.
b) Which trigonometric ratio can be used to determine the length of the piece of
wood?
c) Determine the length of the piece of wood.
|
|
|
2.
|
A bicycle tire revolves at 150 rpm (revolutions per minute). What is its angular
velocity, in radians per second, rounded to two decimal places?
|
|
|
3.
|
Sketch the graph of 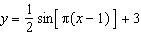 for two cycles, where angles are in
radians.
|
|
|
4.
|
The table shows the fraction of the Moon that can be seen at midnight from
Simone’s town. Day 1 represents January 1. Day | 1 | 2 | 3 | 4 | 5 | 6 | 10 | 14 | 19 | 21 | Fraction
Visible | 0.25 | 0.17 | 0.12 | 0.06 | 0.02 | 0.00 | 0.10 | 0.56 | 0.98 | 1.00 | | | | | | | | | | | |
| Day | 24 | 30 | 35 | 41 | 45 | 51 | 56 | 60 | 65 | 66 | Fraction
Visible | 0.78 | 0.33 | 0.02 | 0.15 | 0.65 | 1.00 | 0.78 | 0.30 | 0.01 | 0.00 | | | | | | | | | | | |
a) What is the period of the sine function that could be used to
model the data? b) What is the amplitude of the function? c) What is the phase
shift of the function? d) What is the vertical shift? e) Use your answers to
parts a) to d) to write an equation for the function. f) Use your function to determine the
fraction of the moon visible to Simone on day i) 100 ii) 150 iii)
200
|
|
|
5.
|
A sinusoidal function has an amplitude of 2, a period of 180°, and a
maximum at (0, 4).
a) Represent this function with an equation using a sine
function.
b) Represent this function with an equation using a cosine function.
c)
Explain how these two functions are related.
|